基于容量价值函数的综合能源系统多元资源协同配置

摘要

综合能源系统（integrated energy system，IES）是实现“双碳”目标的重要载体，而经济、高效的多元资源协同配置是实现综合能源行业持续健康发展的前提。目前，IES配置模型多以成本最小为优化目标，而对投资回报率的考量较少，这可能导致成本回收期延长，进而降低资金周转效率并增加财务风险。有鉴于此，首先，提出IES容量价值函数，该函数以待配置资源容量为自变量，以系统运行成本降低量为因变量，实现多元资源容量价值的解析表达。然后，建立一种基于分式规划理论的多元资源协同配置模型，该模型以最大化投资收益率为目标，旨在构建具有最佳成本效益的配置策略。进一步地，通过变量替换技术将难以求解的分式规划问题线性化，并提出一种分解迭代算法，实现容量价值函数的外逼近与多元资源协同配置策略的高效求解。最后，通过仿真分析以及与成本最小法的对比，验证所提方法的有效性。

01 风-光-储-电-热IES运行模型

本文考虑的IES基本框架如图1所示。系统能源供给由光伏电站、风电场和外电网组成，为电锅炉及电负荷供电，储能设备根据可再生能源发电情况进行充放电，当可再生能源发电不足时由外电网补偿电能；电锅炉通过电-热转换提供热能以满足热负荷需求。

图1  综合能源系统结构

Fig.1  Structure of IES

设置步长为t、运行周期为T，则IES系统的功率平衡约束为

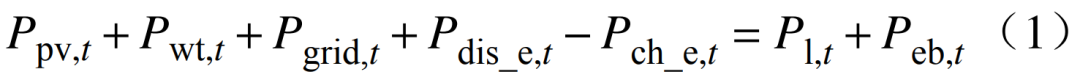
式中：、分别为光伏电站和风电场在t时刻的输出功率；为t时刻电网的输出功率；、分别为t时刻储能装置的放电和充电功率；为电负荷功率；为电锅炉的输出功率。

风电场和光伏电站的出力约束分别为

式中：δwt,t、δpv,t分别为风电和光伏发电在t时刻的归一化出力；Cw、Cp分别为风电场和光伏电站的装机容量。

储能装置考虑能同时充放电的情况，约束为

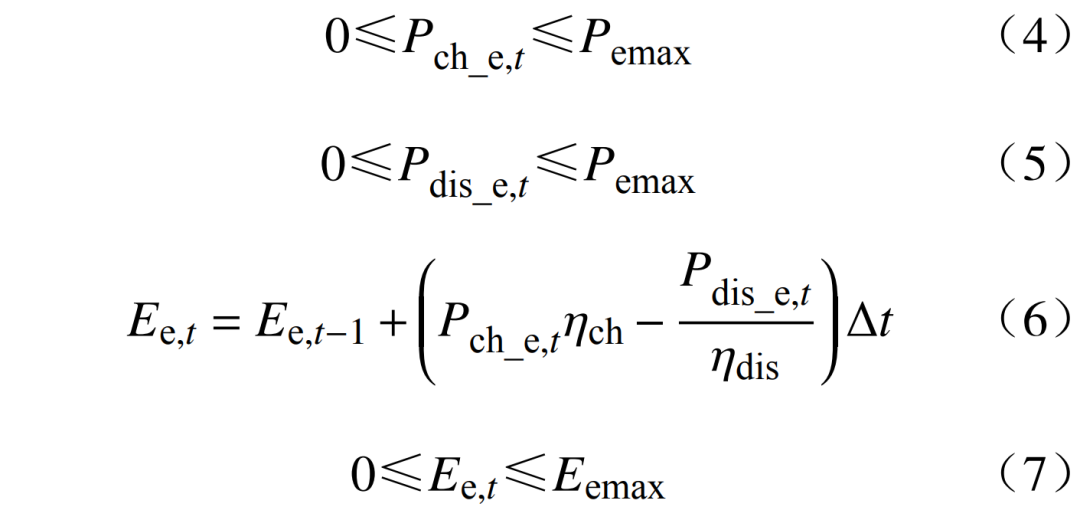
式中：为储能装置的最大充放电功率；ηch、ηdis分别为储能装置的充、放电效率；Ee,t为储能装置在t时刻的蓄电量；Eemax为储能装置最大容量。

热负荷平衡约束为

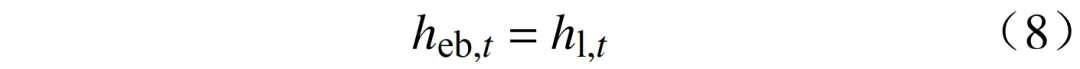
式中：heb,t为t时刻电锅炉的输出热功率；hl,t为t时刻的热负荷。

电锅炉约束为

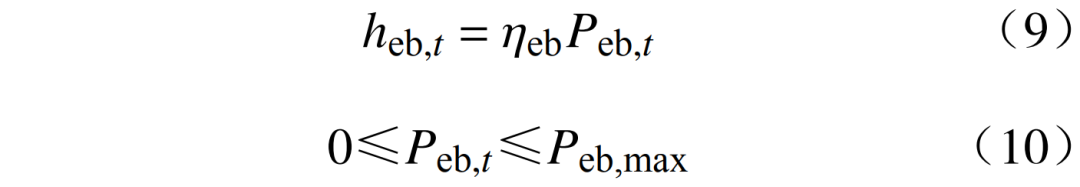
式中：ηeb为电锅炉的热-电转换效率；Peb,max为电锅炉的最大输出功率。

02 IES容量价值函数

由于IES中配置风电、光伏和储能装置，系统的运行成本得以降低，为探究多元资源容量配置对运行成本的影响，建立容量价值函数模型。

本文中电网购电的电价采用峰谷电价，高峰期TH时段内电价为λh，低谷期TL时段内电价为λl，则IES的日运行成本为线性规划问题，即

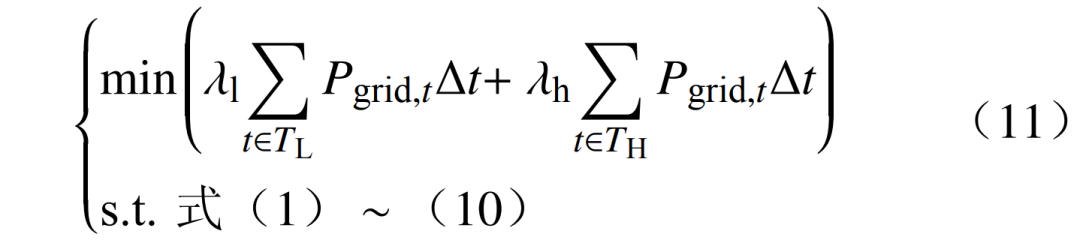
为简便，将问题（11）写为矩阵形式，即

式中：

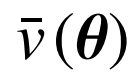
为运行约束条件下IES的最低日运行成本；=

Cw Cp Eemax ，为待配置参数；

为系统运行的决策变量向量；

为系统运行约束对应的常系数矩阵，

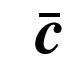
为目标函数对应的常系数矩阵；Θ为待配置参数的可行域，表示所有满足投资预算及容量约束的

Cwmax和Cpmax可以通过历史风速和光照强度计算得到当地风光资源量，并根据建设地区面积限制得到装机容量上限。

由于新能源发电和负荷侧的不确定性，右侧约束项

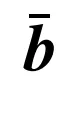
是未知的。选择S个概率为ρs的典型日（s=1:S）来构建不同场景。式（12）在第s个场景下为

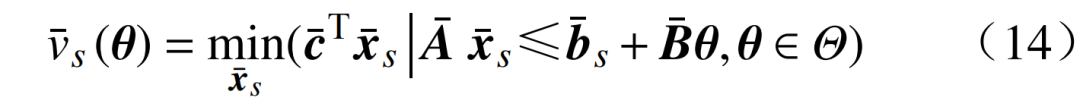
综合所有不同场景，日运行成本可表示为

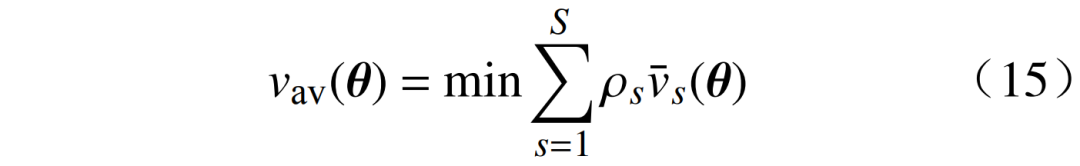
可将式（15）表示为更简洁的形式，即

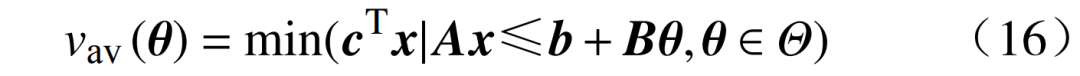
式中：

、、和为汇总每个场景后的常系数。

定义V()为容量价值函数，该函数表示了IES中待配置参数在不同配置容量下，系统所减少的运行成本，以体现各资源在系统运行中的容量价值，即

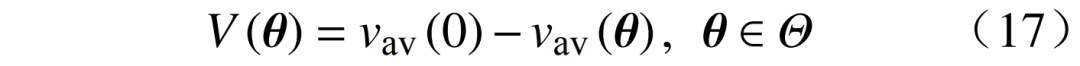
式中：vav(0)为未配置风电、光电和储能装置的日运行成本。

03 基于分式规划的多元资源协同配置方法

3.1  分式规划模型

本文考虑投资回报率最大化的多元资源协同配置方法，系统的投资成本表示为

式中：Cin为总投资成本；κw为风电场的单位装机容量成本；κp为光伏电站的单位装机容量成本；κe为储能装置的单位容量成本；κep为功率器件的单位成本；κ0为部署风电、光电、储能装置的固定成本，包括运输成本和安装成本。

由于未配置风电、光电和储能装置时所有负荷需要电网供电，因此运行成本vav(0)最高。当⩾0时，一定有vav(0)⩾vav()。本文规划模型的目标是使降低的日运行成本与投资成本的比率最大化，即

当=0时，目标函数值为0；当足够大时，vav()为常数，投资成本Cin很大，目标函数值很小。因此目标函数一定存在最大值。若目标最优值为，则1/为最小回报时间，即在最短时间内，通过降低运行成本实现投资成本回收。

解决式（19）有2个困难。1）缺乏vav()的显式表达式，2）目标函数具有非凸性。由于

3.2  最优值函数近似

为了解决问题式（19），首先讨论vav()的近似函数。式（16）的对偶形式为

由于强对偶性，式（20）的最优值等于式（16）的最优值。在式（20）中，vav()是无穷多个仿射函数在的点极大值。由于点极大值保持凸性，vav()是凸函数，−vav()是凹函数。目标函数式（19）中，分子为凹函数，分母为正线性函数，可行区域是多面体，则目标函数是伪凹的，局部最大值点就是全局最大值点。若vav()可以近似，则可以使用局部算法求解目标函数式（19）。

确定了vav()的凸性，若有足够多的采样点，是问题式（20）的最优解，将式（20）中的v()用标量变量ζ代替，在规划模型的约束条件中添加以下的切割平面。

vav()与切割平面相交于，所以vav()可以用附近的值近似。

3.3  分式规划问题线性化

当vav()通过切割平面得到近似值，规划模型变为如下形式。

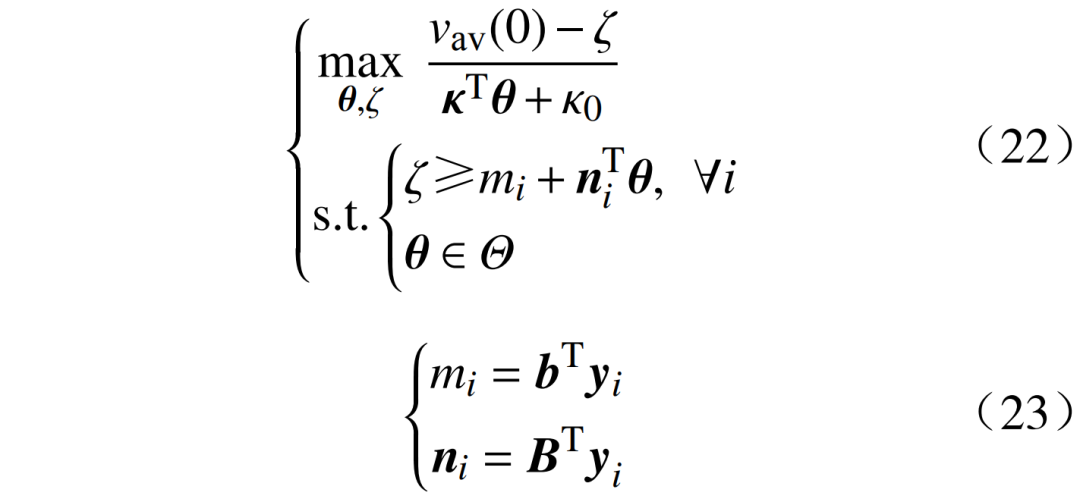
由于3.2节提到的伪凸性，此问题可以通过局部算法来解决，但也可以将其转化为线性规划问题。与使用非线性规划求解器解决非凸优化问题相比，求解线性规划更简便。定义新变量

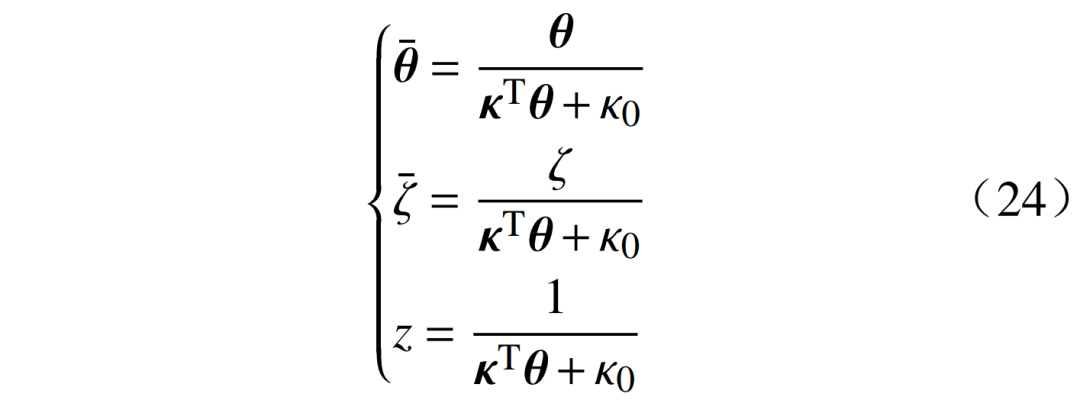
则有

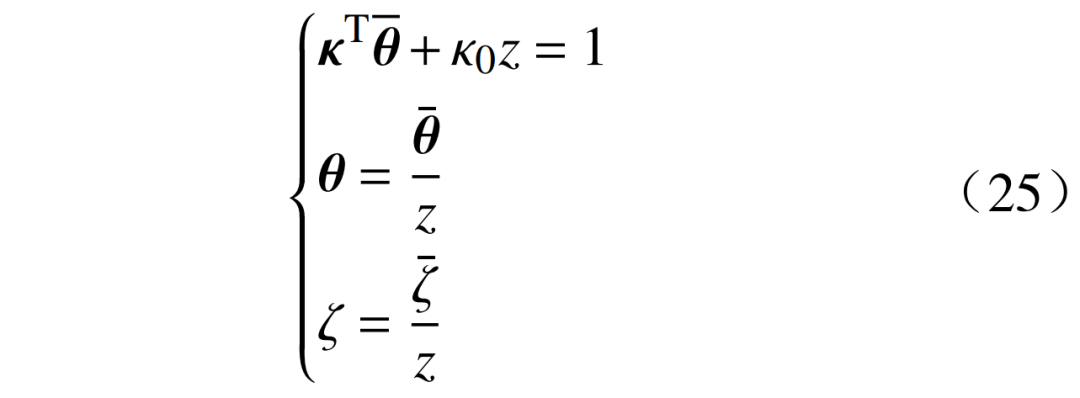
式（22）转化为如下线性规划问题。

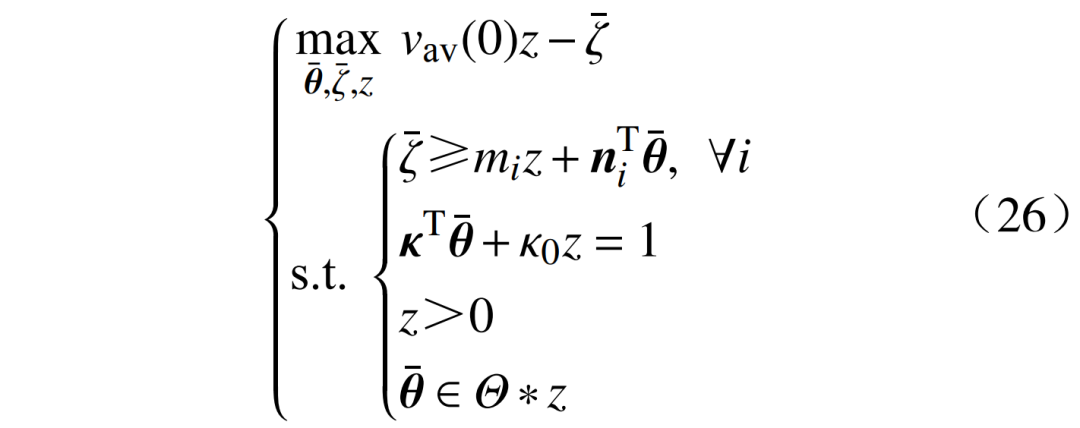
式（22）通过变量替换，等效转换为式（26），两者具有相同的最优值。式（22）的最优解可以通过式（26）的最优解进行变量转换，从而得到的最优配置。

3.4  分解算法

本文提出一种分解算法，将需要求解的问题分解为主问题和子问题，主问题式（26）通过变量替换将分式规划问题线性化，子问题式（20）根据式（21）生成的切割平面来近似最优值。在迭代过程中，对切割平面集进行更新，算法流程如图2所示。

图2  算法流程

Fig.2  Algorithm process

当问题式（26）中有更多的切割平面时，可行区域缩小，最优值是个递减序列，且目标函数是有界的，所以算法必定收敛。

切割平面式（21）将问题分解为对偶形式式（20）和线性规划问题式（26），这两个问题都容易解决，因此算法是高效的。

04 案例分析

本文选取每个季节两周、56个典型日、t=1 h建立规划模型。电价如表1所示。风光装机容量上限

表1  电价设置

Table 1  Tariff setting

4.1  配置方案分析

经过算法迭代收敛，配置结果为风电装机容量Cw=32.34，光伏电站装机容量Cp=17.05，储能容量Eemax=26.09⋅，储能装置最大功率Pemax=5.46kW。此配置方案下，日运行成本下降201.9元，天可将投资成本回收。

图3展示了容量价值函数在多个采样点的数值变化，其中设定储能装置额定充放电时间为3小时，即

图3  容量价值函数

Fig.3  Capacity value function

由此可见，容量配置时，风电对运行成本的影响最大，光伏次之，储能装置影响最小。由于风电和光伏作为IES的主要供能单元，对运行成本影响较大，而光伏电站在夜晚不能出力，因此光伏对运行成本的影响比风电低；储能装置作为辅助装置，只能储存多余的风能和太阳能，提供的能量较少，因此对运行成本影响最小。

4.2  灵敏度分析

通过改变各个投资参数，观察各参数设置对回收天数的影响，结果如表2~5所示。

表2

Table 2  Impact of κw

表3

Table 3  Impact of κp

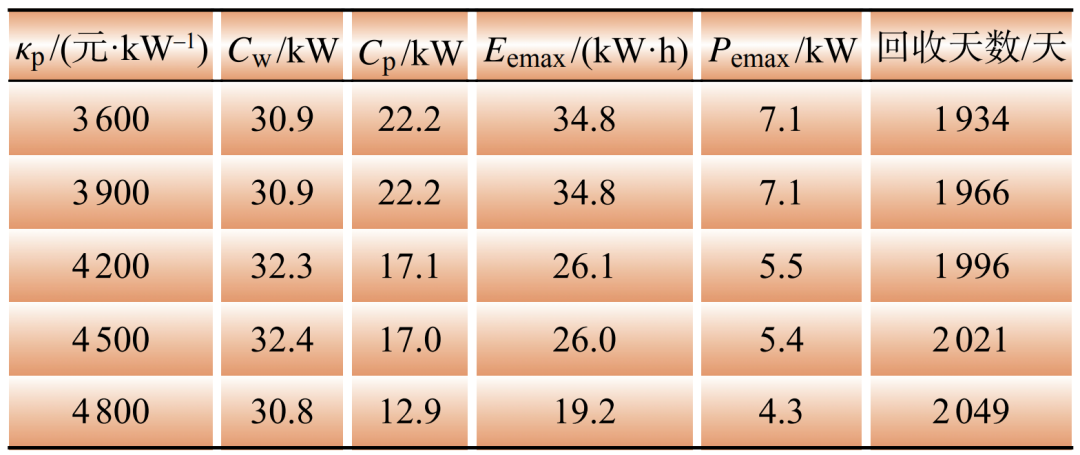
表4

Table 4  Impact of κe

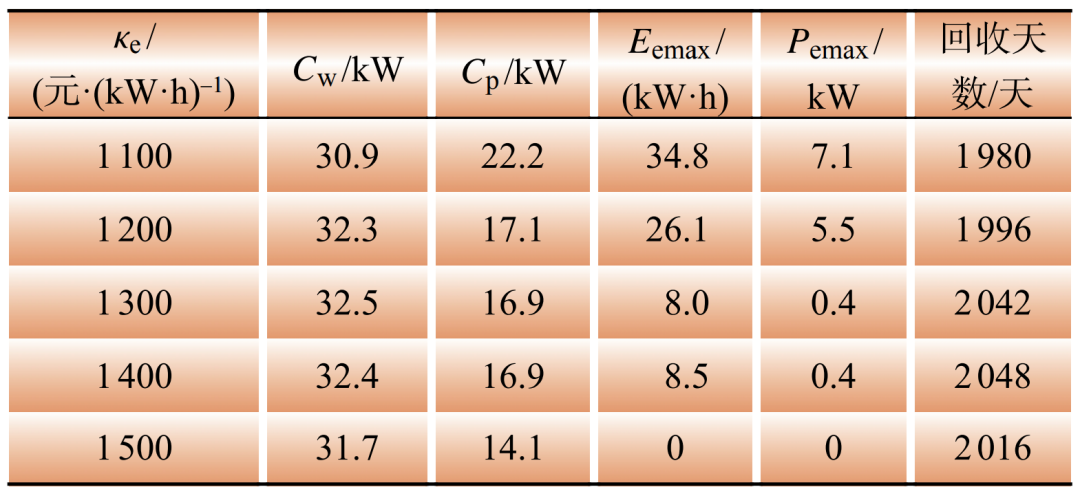
表5

Table 5  Impact of κep

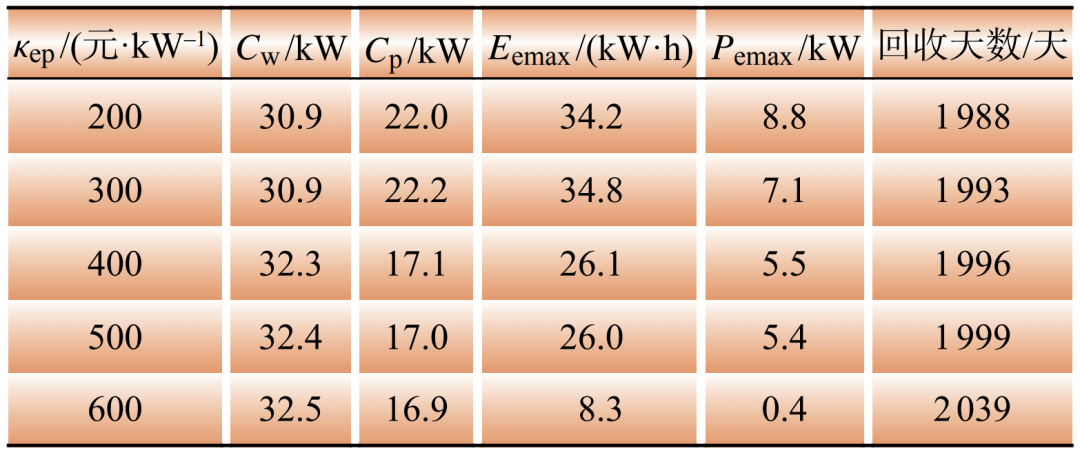
风电、光伏和储能装置功率的配置容量都随着各自投资参数的增加而降低，回收天数也增大，可能是由于投资参数增加，投资成本增大，而导致规划模型比值恶化，成本回收期更长；κp为~元/kW时，配置容量不变，表明在此范围内，该容量配置是最优的；而

4.3  对比分析

将本文提出的规划模型与常用的成本最小模型进行对比，成本最小模型为

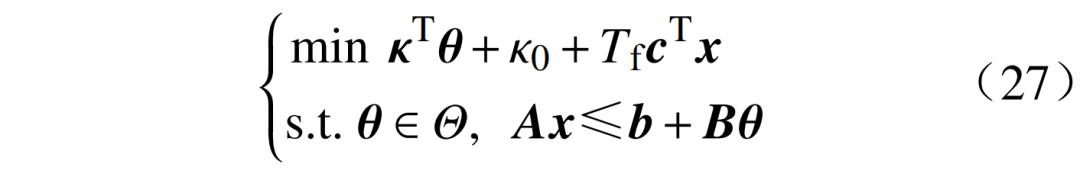
式中：Tf为设备的使用寿命（天数）。成本最小模型旨在整个寿命周期内，找到投资成本与运行成本之和最小的配置策略。

本文从投资成本、运行成本和利润方面对比2种方法，其中总运行成本为Tfvav()，利润定义为T，结果如图4~5所示。

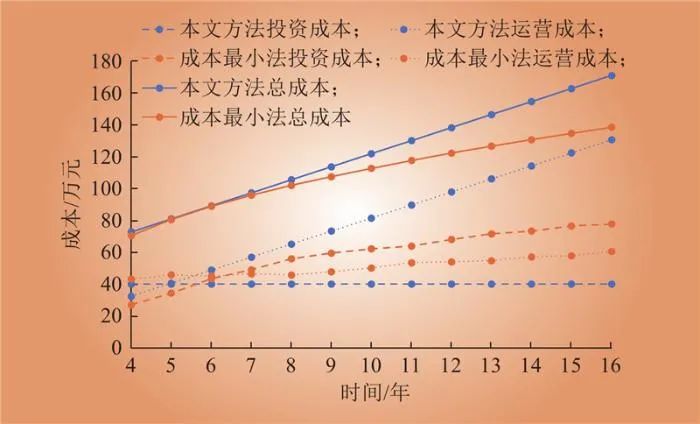
图4  本文方法与成本最小法的成本比较

Fig.4  Cost comparison between proposed method and cost- minimization method

图5  本文方法与成本最小法的利润比较

Fig.5  Profit comparison between proposed method and cost- minimization method

由于本文配置模型的投资规模与Tf无关，因此不同使用寿命下的建设规模与投资成本不变；使用寿命从第6年开始，成本最小法的投资成本超过本方法，同年，运行成本小于本文方法的运行成本；成本最小法的总成本始终小于本文方法，在第6年时总成本差距最小，仅元，之后使用寿命越长，差值越大。由于成本最小法追求更小的总成本，因此在建设初期需要更多的投资成本，增大配置容量，使后期的运行成本降低。

在利润及回报率方面，由于从第6年开始，成本最小法的运行成本更低，利润也更高；本文方法由于配置规模不变，利润呈线性增长；本文方法的回报率始终大于成本最小法，但在4~8年的使用寿命下，本文方法的回报率比成本最小法的回报率高不到10%，从第9年开始，使用寿命越长，回报率差值越大，投资回收效果越明显，若使用寿命为16年，两者的回报率相差51.35%。

综上，成本最小法通常投资较大的规模，导致更高的投资成本，但降低了运行成本，总成本更小；本文方法投资成本较小，虽然运行成本更高，但能得到较高的回报率，在短期内优势不明显，在长期使用的情况下，如9年及以上，本文方法的成本回收效益明显更好，适合初期建设资金有限，追求快速回收成本的投资者。

4.4  算法效率对比

由于本文通过多个采样点的切割平面集逼近最优值，因此使用均匀分布采样方法在待配置参数的四维空间均匀采样，取多组数据，与本文的求解方法进行对比，结果如表6所示。

表6  迭代算法与均匀分布采样法效果对比

Table 6  Comparison of the effectiveness of the iterative algorithm and the uniformly distributed sampling method

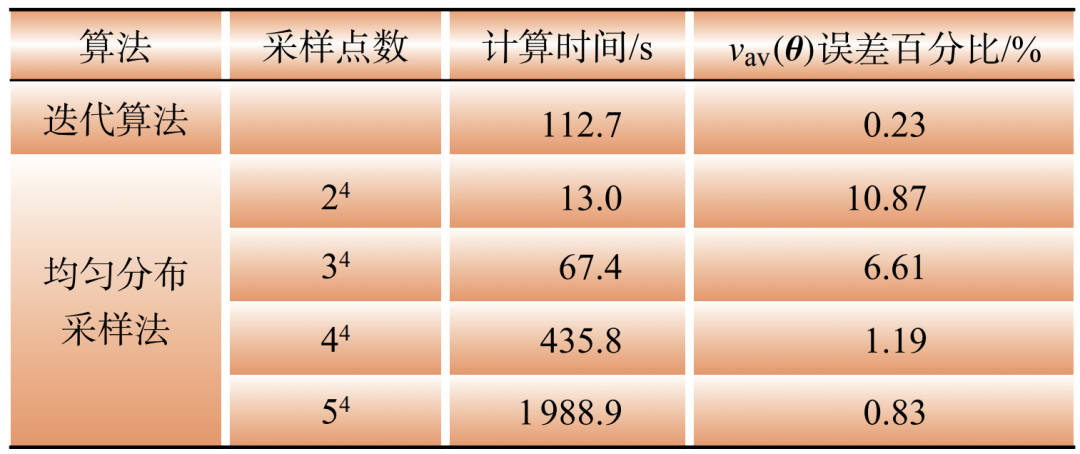
由表6可知，均匀分布采样方法在采样点较少时，对

05 结论

本文提出了一种基于分式规划理论的多元资源协同配置模型，并使用分解迭代算法进行求解。经过算例分析验证所提模型和方法的有效性，主要研究结论如下。

1） 本文提出的分解迭代算法通过自适应寻优，在最优解附近逐渐逼近，以较少迭代次数实现高精度求解，并显著降低计算时间。相较于均匀分布算法，该算法避免了采样点不足导致的精度下降以及采样点增加带来的计算效率低下问题，可高效求解多维优化问题。

2） 本文模型可实现成本回收效益最优的多元资源配置，适用于初期资金有限且追求高回报率的投资者，并在长期运行中展现更优的投资回报效果。相比之下，成本最小模型在总成本控制方面更具优势，尤其在短期运行系统中更具吸引力，适合于追求最低总成本的投资者。

本文模型为投资者提供了一种新策略，便于其在不同投资目标和运行周期下做出相应决策。然而，该模型仍有进一步完善的空间。本文研究主要针对用户侧综合能源系统，未考虑更复杂的能源网络特性。未来研究将扩展至区域级综合能源系统，引入天然气网和热网等多能源设备，丰富模型结构，进一步探索电-气-热多能协同配置方法，从而拓展模型的适用范围。