考虑供电设备差异化报价的虚拟电厂电能量-调峰联合市场优化策略

01

VPP参与电能量-调峰联合市场模型

1.1  电能量-调峰联合市场双层架构

基于双层模型的电能量-调峰联合出清的VPP交易框架如图1所示。VPP参与电力市场的报价模型中，上层主体为电力市场，下层主体包含多个独立运行的VPP和火电机组。下层模型在交易申报阶段，VPP内部所有具备供电能力的资源向VPP运营商进行电价与电量的申报，燃气机组额外向VPP运营商申报调峰电价与调峰电量，各VPP运营商统筹内部单元的申报参数上报至电力市场；上层模型在交易出清阶段，电力市场以出清成本最小化为目标，以日前市场负荷曲线为约束条件进行出清。各VPP运营商根据出清结果向内部各单元颁布调度电量。经过多次迭代后，使上下层联合收益最优的申报参数和出清结果即为日前最优交易计划。

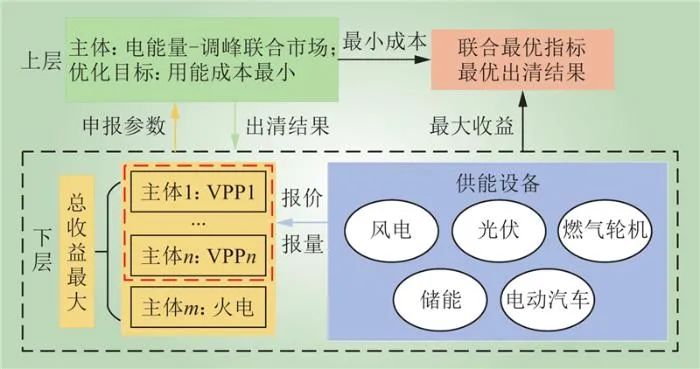
图1  VPP交易双层架构

Fig.1  Dual-layer frame work of VPP transaction

虚拟电厂参与日前电能量-调峰市场报价流程如图2所示。各虚拟电厂和火电厂在竞标报价之前，须进行自身优化并做出报价决策，向电力市场多轮次提交能量、调峰出清功率曲线及价格。在市场关闭后，电力市场组织出清并进行系统安全校核，通过后电力市场公布各虚拟电厂和火电厂机组出清信息。各虚拟电厂须按照市场交易结果安排机组出力，并按照报价进行收益结算。

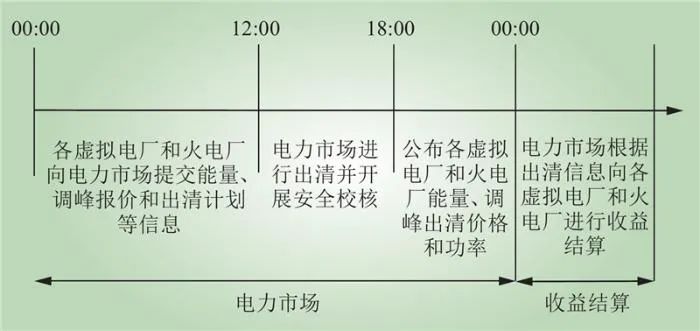
图2  VPP参与电能量-调峰市场报价流程

Fig.2  The quotation process for VPP participating in electric energy-peak regulating joint market

1.2  VPP内部供电设备差异化报价机制

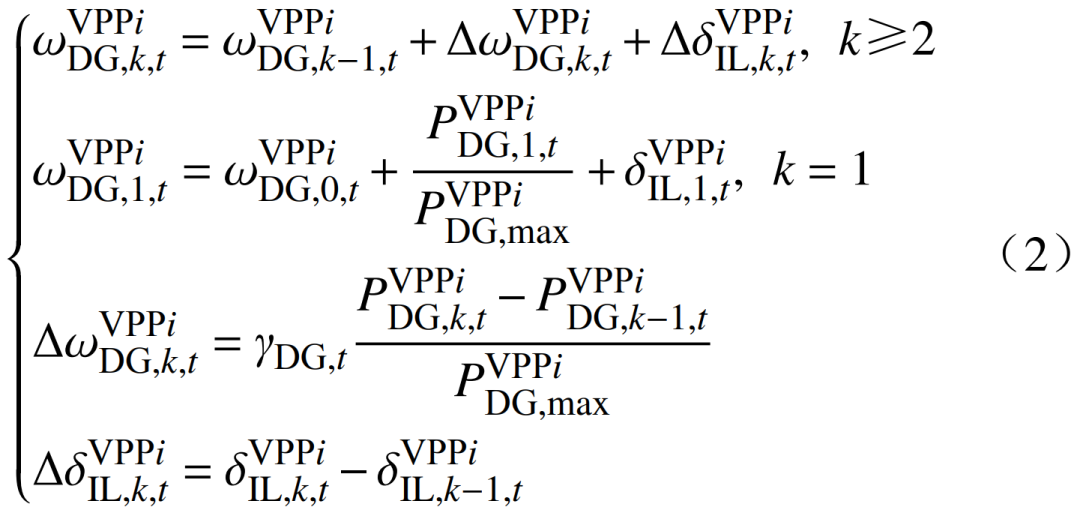
VPP内部供电设备通过多次报价获得最优出清功率，本节所提差异化报价机制模型建立起了VPP内部供电设备多次报价之间的动态联系，供电设备可以根据上一次报价信息动态调整下一次报价，进而实现上下层利益的动态均衡；由需求价格弹性理论描述供需关系可知，价格随着需求的增大而提升。各机组出力与市场负荷需求呈正相关，出力越大，申报价格越高，本文运用上述价格与功率之间的关系进行各机组申报价格的制定；此外，所提报价机制模型考虑绿证、需求响应等因素对价格的影响，使VPP内部资源供电设备报价机制模型中包含更多信息，提升VPP内部供电设备资源报价对各供电设备成本特性的刻画能力。其中，碳排放量对下层虚拟电厂各设备报价的影响起到正向增加的作用，即下层虚拟电厂碳排放量越高，燃气机组报价提升；绿证收益对下层虚拟电厂各设备报价的影响起到负向降低的作用，即绿证收益越大，新能源机组报价越低；负荷需求响应对下层虚拟电厂各设备报价的影响起到正向增加的作用，即需求响应越大代表虚拟电厂功率不足，虚拟电厂内部各设备通过提高报价减少出清维持自身功率平衡。上述3种因素动态调节、相互作用，影响下层虚拟电厂各设备报价。

1.2.1  供电设备报价成本系数模型

本文结合碳交易、碳-绿证互认机制和绿证交易模型建立碳交易和绿证价格系数模型为

式中：

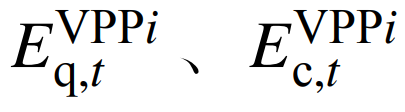
分别为VPPi在时刻t的核算碳排放量、碳配额和净碳排放量；η为碳-绿证互认因子；

为绿电消纳功率；π为碳交易价格；l为碳交易区间长度；ξ、τ分别为碳交易奖励和惩罚因子；μ为绿证价格；β、ω分别为绿证奖励和惩罚因子；χ、

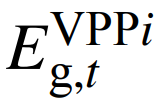
分别为绿证区间长度和绿证数量；

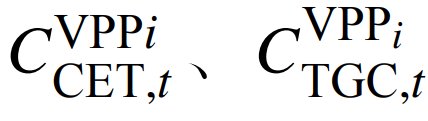
分别为碳交易和绿证收益或成本；

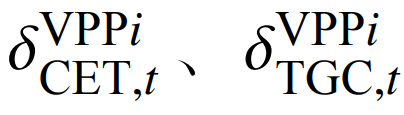
分别为碳排放交易和绿证交易折算的价格系数；

为燃气机组功率上限。

负荷中断受到用户非理性因素的影响，导致不能准确获取负荷中断功率。基于此，本文引入前景理论来描述负荷参与需求响应的感知收益，建立负荷中断价格系数模型。

1.2.2  供电设备报价机制

本文各设备均同时参与能量市场和调峰市场，两种价格的制定原理、模型一致，不同点在于各设备初始价格不同。此外，火电机组独立于VPP存在，可以直接向电力市场报价，因此，本文不再单独建立火电机组报价机制。

1）新能源机组报价机制为

式中：

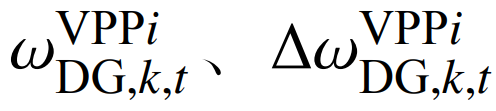
分别为VPPi在时刻t的第k次新能源机组报价和前后两次报价差值；

分别为第k次报价的负荷中断价格系数和前后两次报价系数差；

为新能源机组初始价格，由新能源机组运维成本、折损成本等组成；

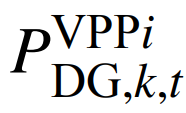
为第k次报价的新能源发电功率；

为新能源发电功率上限；γDG,t为新能源机组价格调节系数。

2）燃气机组报价机制为

式中：

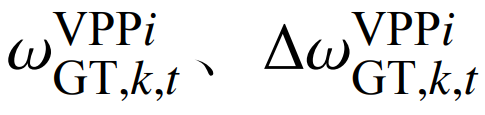
分别为VPPi在时刻t的第k次燃气机组报价和前后两次报价的差值；

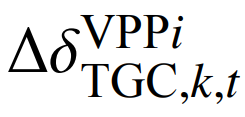
分别为前后两次报价的碳交易和绿证价格系数差；qprice,t、ηGT和Vgas分别为分时气价、燃气机组效率和天然气热值；

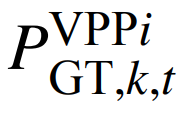
为第k次报价的燃气机组功率；

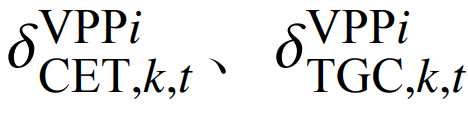
分别为第k次报价的碳交易和绿证价格系数；γGT,t为燃气机组价格调节系数。

3）储能/电动汽车报价机制为

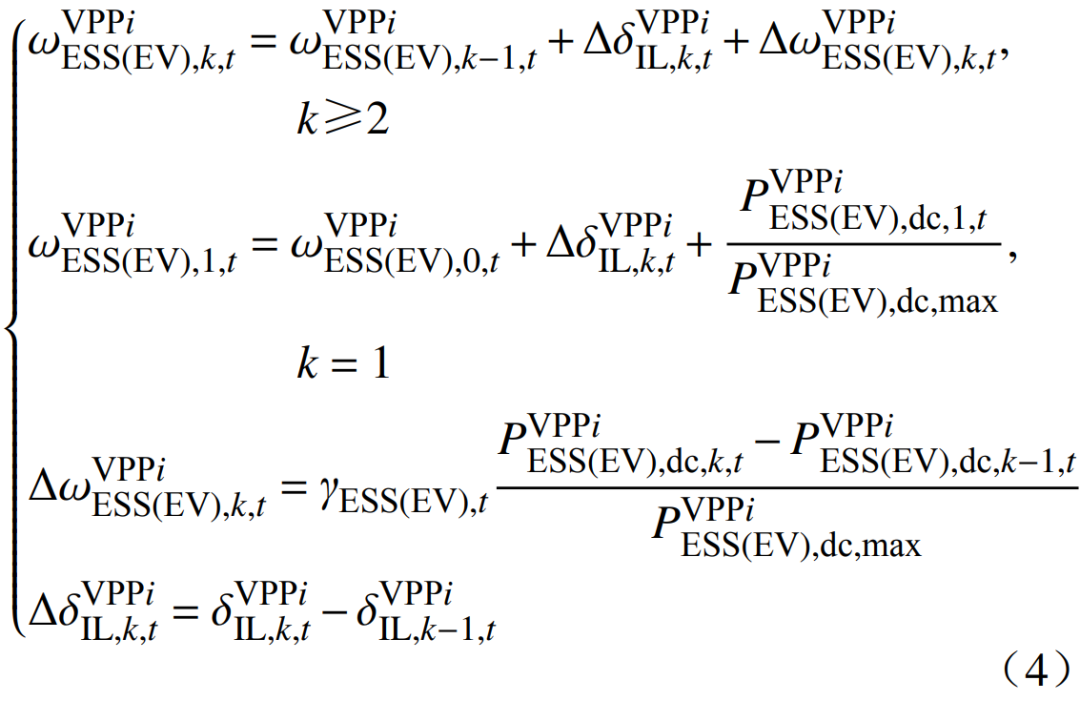
式中：

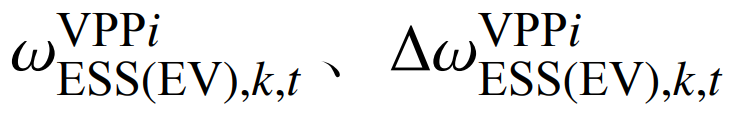
分别为VPPi在时刻t的第k次储能/电动汽车报价和前后两次报价差值；

为储能/电动汽车的初始价格；

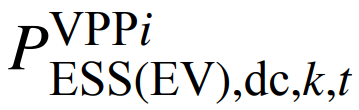
为第k次报价的储能/电动汽车放电功率；

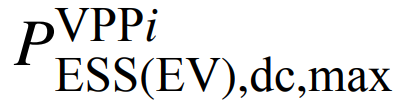
为储能/电动汽车放电功率上限；γESS(EV),t为储能/电动汽车的价格调节系数。

4）报价约束。为防止下层VPP和火电机组在价格申报过程中出现恶意报价和串谋报价的行为，对下层不同设备报价上、下限进行差异化约束，即不同设备报价上下限不同，具体约束为

式中：

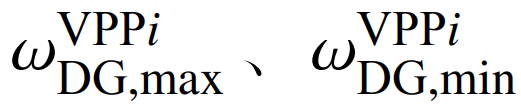
分别为VPPi新能源机组发电价格的上、下限；

为燃气机组价格的上限；

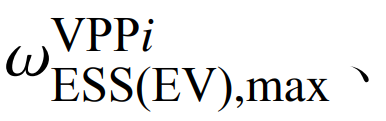
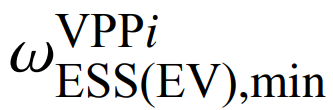
分别为储能/电动汽车放电价格的上、下限；ωG,max、ωG,min分别为火电机组价格的上、下限。

5）报价加密模型。采用带阈值解密的密码系统（paillier cryptosystem with threshold decryption，PaillierTD）对VPP内各设备的最优报价、功率等信息进行加密， PaillierTD算法设计可以分为3个部分。

VPP向各设备发布密匙，通过对各设备报价进行加密后传输至VPP，VPP对各设备报价解密后传输至电力市场，该方法避免了各设备报价信息泄露的风险。

02

VPP参与电能量-调峰联合市场双层优化模型

2.1  上层模型

目标函数为上层出清成本Fmarket最小，即

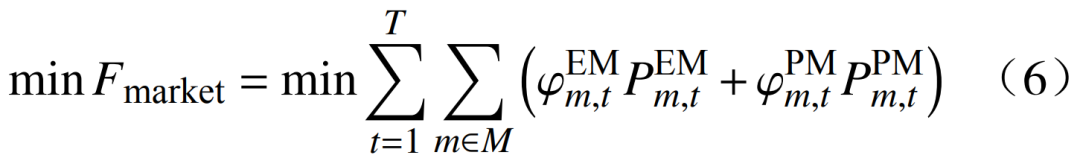
式中：T为调度周期；M为{DG, GT, ES, EV}组合，分别指新能源机组、燃气机组、储能和电动汽车；

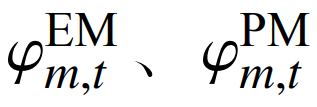
分别为设备m在时刻t的出清价格和调峰价格；

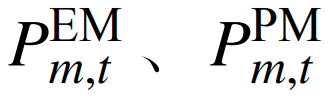
分别为设备m的出清功率和调峰功率。

同时应满足功率需求平衡约束。

2.2  下层模型

以总成本最小化为目标，建立下层多VPP参与电能量-调峰联合市场的报价模型为

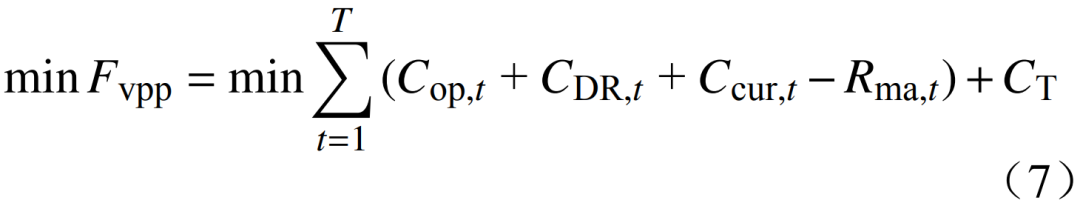
式中：Fvpp为下层VPP的总成本；Rma,t为下层参与联合市场交易在时刻t的总收益；Cop,t为下层VPP的总运行成本；CDR,t、Ccur,t分别为下层VPP的需求响应和弃风弃光惩罚成本；CT为下层VPP的储液罐折旧成本。

1）联合市场收益为

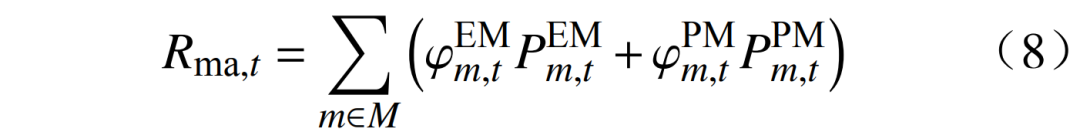
2）VPP运行成本为

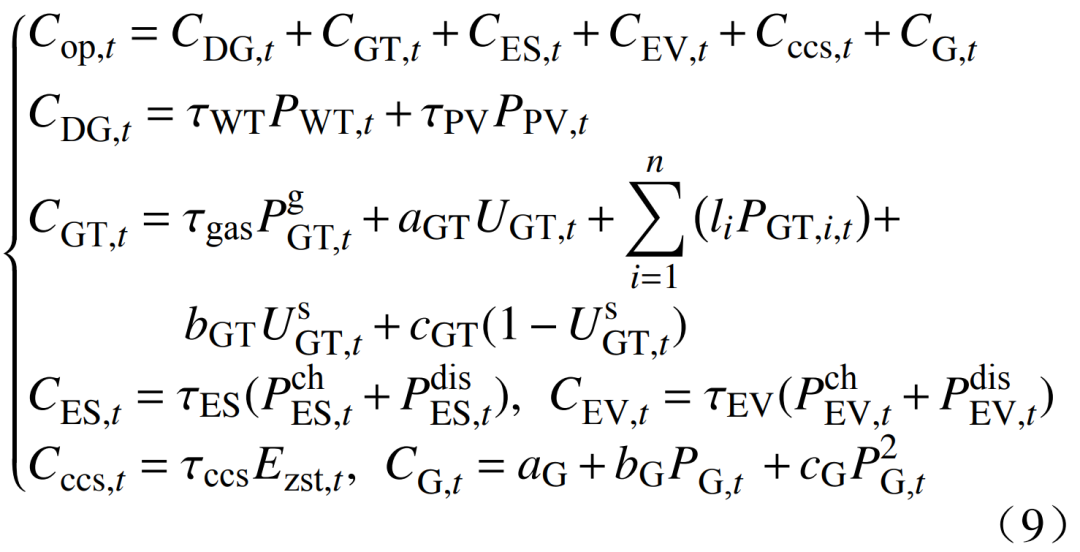
式中：、、、、和分别为新能源机组、燃气机组、储能、电动汽车、碳封存系统和火电机组在时刻t的运行成本；

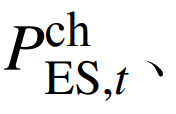
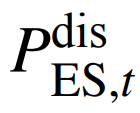
分别为电储能在时刻t的充、放电功率；

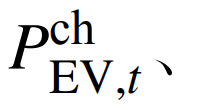
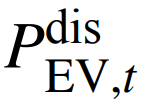
分别为电动汽车在时刻t的充、放电功率；为时刻t碳捕集可再生塔中处理的二氧化碳量；τWT、τPV、τgas、τES、τEV和τccs分别为风电、光伏、购气、储能、电动汽车和碳封存的成本系数；aGT、bGT、cGT分别为燃气机组运行、启停的成本系数；

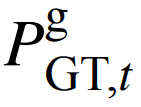
为时刻t向燃气轮机供给的天然气功率；li为燃气机组第i段线性化成本斜率；PGT,i,t为燃气机组第i段线性化功率；为碳捕集再生塔处理的二氧化碳量；aG、bG、cG分别为火电机组成本系数。

3）需求响应成本为

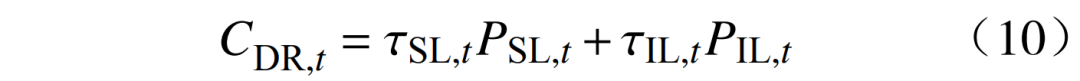
式中：τSL,t为时刻t的分时电价；τIL,t为时刻t的可中断负荷的补偿价格；PSL,t、PIL,t分别为时刻t的可中断负荷功率、可转移负荷功率。

4）弃风弃光惩罚成本为

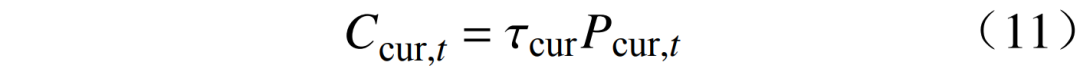
式中：τcur为单位弃风弃光功率的惩罚成本系数；Pcur,t为时刻t弃风弃光功率。

5）储液罐折旧成本为

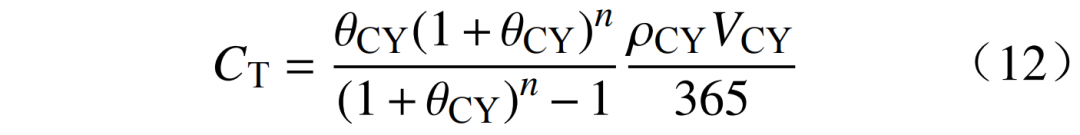
式中：θCY为投资贷款年利率；ρCY为建设单位容量储液罐所需的建设费用；VCY为储液罐额定容量；n为年数。

约束条件包括燃气机组约束、碳捕集设备相关约束、电储能约束、电动汽车约束、功率平衡约束，具体可以参考文献。

2.3  模型求解流程

本文调用CPLEX求解器对双层模型进行求解，为实现双层利益最优，以联合优化目标函数为最优解判据。联合最优解原理可以描述为：联合最优解表示上下层运行成本数值几何距离的远近，两者距离越近，代表上下层之间的利益协调得越好，即

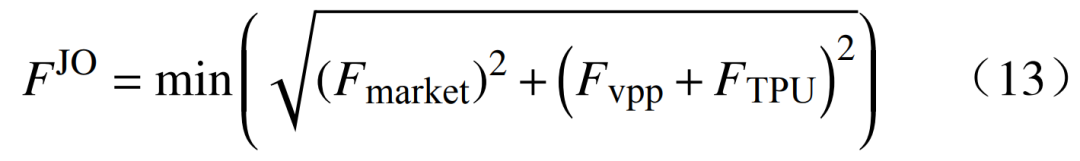
式中：为联合最优成本；F、FTPU分别为下层虚拟电厂和火电机组运行成本。

联合最优解的过程如图3所示，双层模型求解流程如图4所示。

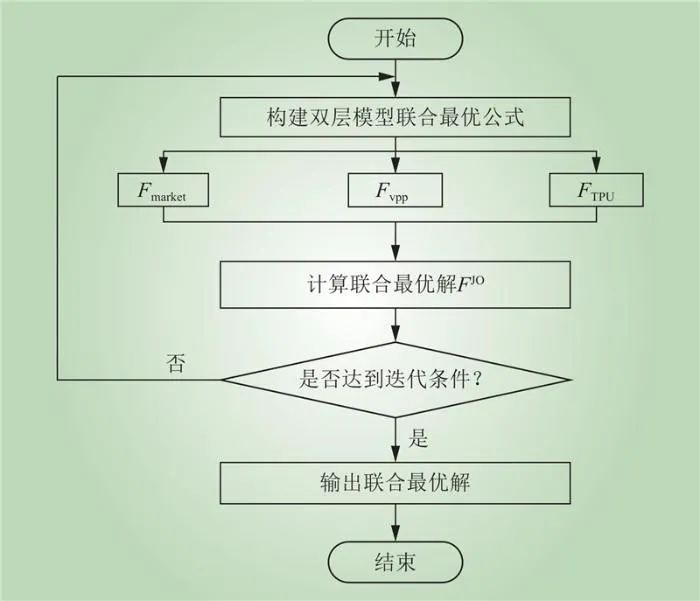
图3  联合最优解求解流程

Fig.3  The Joint optimal solution process

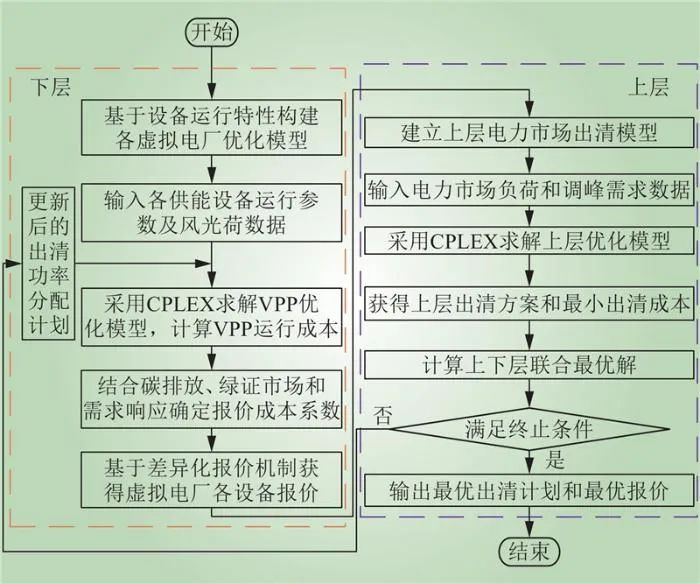
图4  双层模型求解流程

Fig.4  Flowchart of double-layer model

03

算例分析

3.1  参数设置

本文以湖南省江华VPP示范区为例进行算例分析，分时气价参见文献，电力市场与VPP的基础数据如图5~7所示。

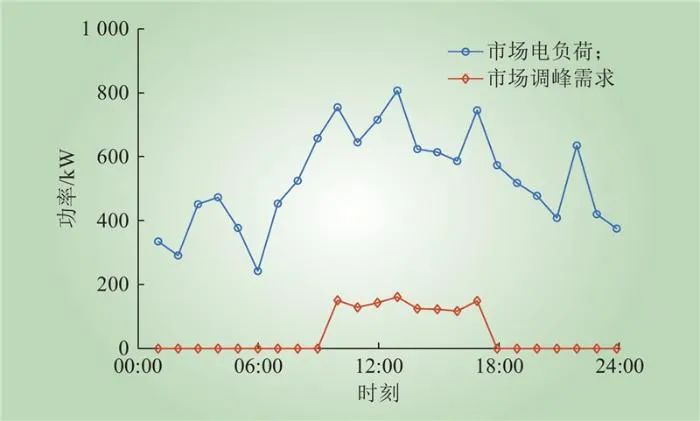
图5  电力市场需求和调峰需求

Fig.5  Electricity market and peak shaving demand

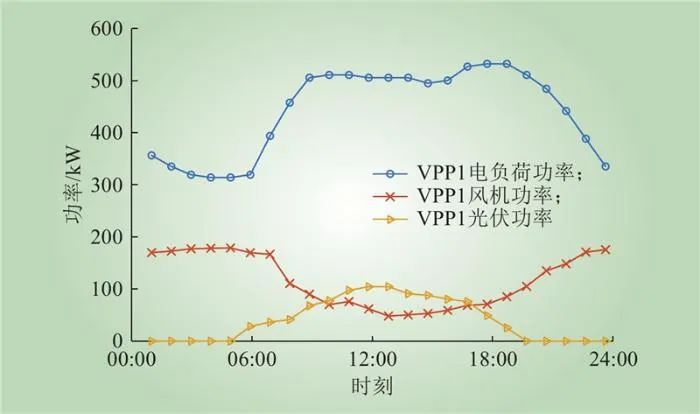
图6  VPP1基础数据

Fig.6  Basic data of VPP1

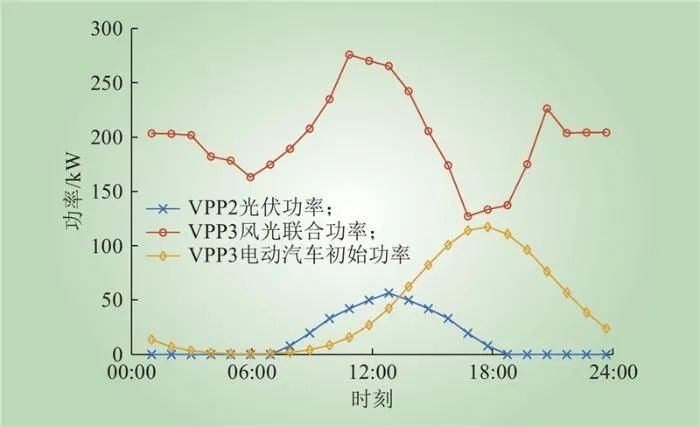
图7  VPP2和VPP3基础数据

Fig.7  Basic data of VPP2 and VPP3

VPP3电动汽车初始充电负荷需求为kW，充电效率为0.95。下层3个VPP均采用阶梯方式描述碳排放价格，基价为0.2元/kg，价格增长幅度为0.25元/kg，每个阶梯的碳排放区间上限均为300 kg；碳捕集设备容量上限为300 kW，捕集系数为3.7 kg/kW；燃气机组的碳排放强度系数为0.4 kg/kW，碳配额系数为0.15 kg/kW，火电机组碳排放强度系数为0.98 kg/kW，碳配额系数为0.7 kg/kW。阶梯碳排放量影响报价的系数上限为0.1元/(kW·h)，负荷需求响应影响报价的系数上限为0.1元/(kW·h)。

3.2  模型求解结果分析

3.2.1  迭代结果分析

VPP参与电力市场双层模型迭代求解过程如图8所示。为提升所提双层模型的实用性，本文设置VPP内各设备报价次数上限为10，即达到10次后迭代终止。从图8可以看出，双层模型在第10次迭代中出现联合最优解，求解时间为1.67 s。其中，上层电力市场运行成本元，下层VPP集群的运行成本为547.65元，联合运行指标为元。此外，可以看出，随着迭代次数的增加，联合指标呈现逐步下降的趋势，代表双层模型通过不断调整VPP内各设备报价，协调了上下层之间的利益关系。在求解过程中，上下层成本呈现出不断波动、此消彼长的规律，主要原因是与下层VPP报价模型相关，双层模型求解是协调上下层利益关系的过程，没有绝对意义的收敛，迭代过程受到报价方式的影响。结合报价机制可以看出，差异化报价与设备出力、碳排放、绿证市场以及需求响应等因素紧密相关，每次迭代过程中，这些因素的变化是没有固定规律的，导致报价的变化在一定的范围内是没有规律的，因此，上下层成本呈现出不断波动的趋势。

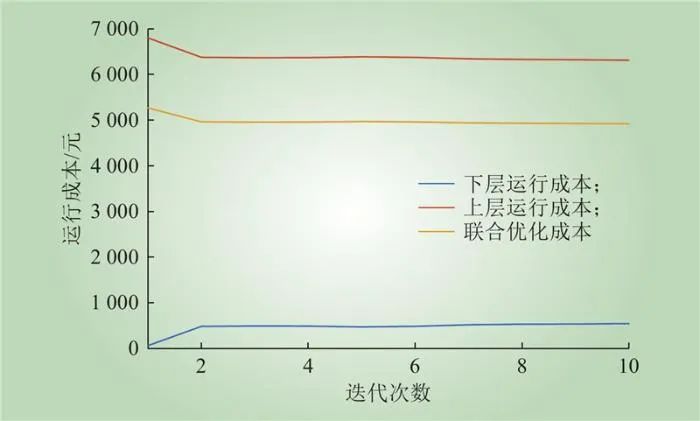
图8  双层模型迭代结果

Fig.8  Iteration results of double-layer model

3.2.2  优化结果分析

本节将下层各VPP最优报价与供电设备最优运行计划作为一组进行分析。VPP1各供电设备最优价格和最优运行计划如图9~10所示。从图中可以看出，燃气机组价格高于其他供电设备价格，而碳捕集设备运行时，能显著降低最优报价。在夜间时段，VPP1通过消耗新能源机组发电，并为电储能充电，缓解其他时段的供电压力；此外，在14:00—16:00，此时负荷处于高峰时段，VPP1通过增大燃气机组出力，维持运行的经济性。在实际应用中，适当提升燃气机组的报价可以降低其退市风险，适当降低新能源机组报价可以提升新能源消纳水平，维持系统运行的经济性。

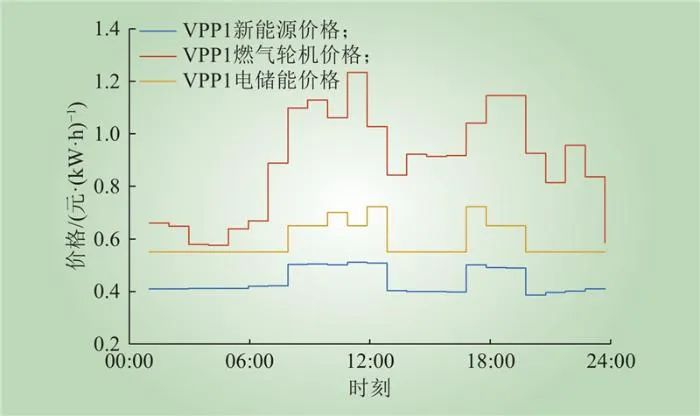
图9  VPP1各供电设备最优报价

Fig.9  Optimal quotation for each equipment in VPP1

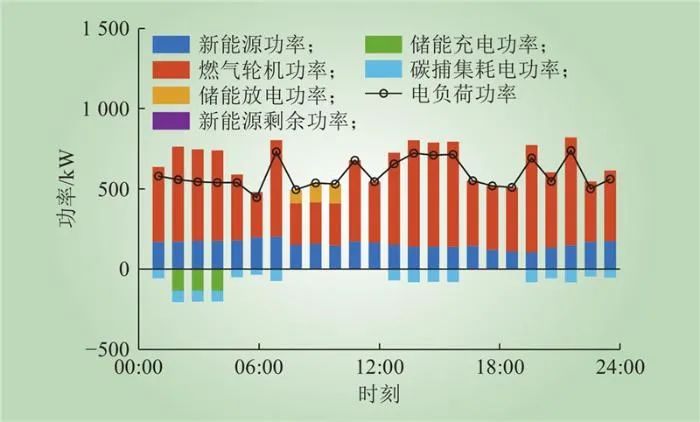
图10  VPP1最优运行计划

Fig.10  The optimal operation plan for VPP1

VPP2各供电设备最优价格和最优运行计划如图11~12所示。在01:00—04:00，天然气价格较低，燃气机组输出电功率并存储于电储能设备中，在16:00—18:00等时段释放。电储能通过低充高放的方式增大了自身的价格优势，为VPP2承担更多的市场功率需求。

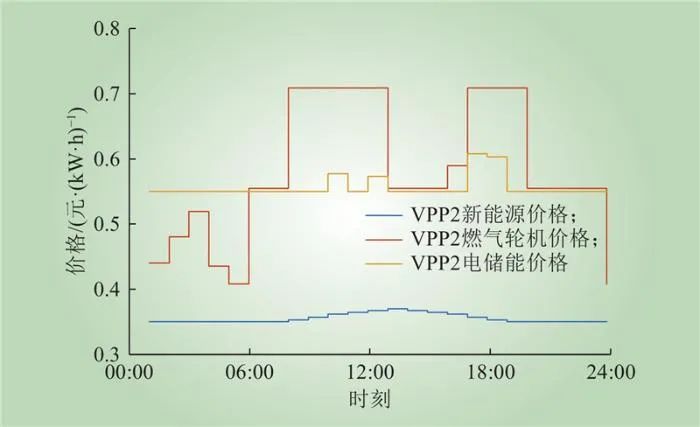
图11  VPP2各供电设备最优报价

Fig.11  Optimal quotation for each equipment in VPP2

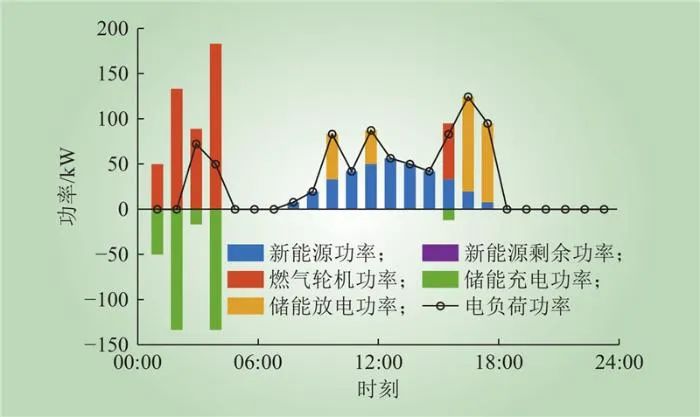
图12  VPP2供电设备最优运行计划

Fig.12  Optimal operation plan for VPP2

VPP3各供电设备最优价格和最优运行计划如图13~14所示。VPP3引导电动汽车在夜间时段充电，这是由于夜间处于市场负荷需求的低谷，并且夜间天然气价格低廉，电动汽车充电需求移入夜间时段可以提升VPP3的运行收益。

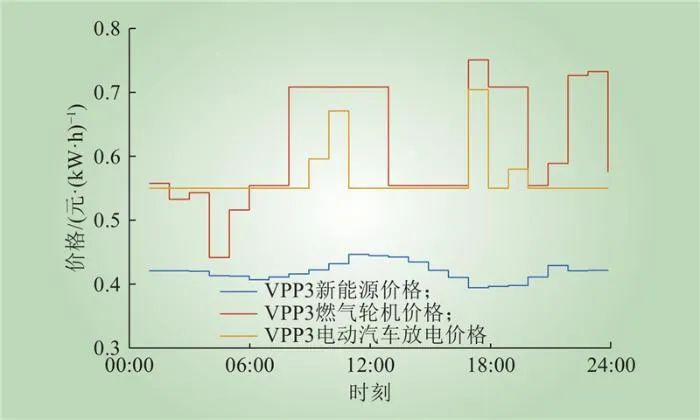
图13  VPP3各供电设备最优报价

Fig.13  The optimal quotation for each equipment in VPP3

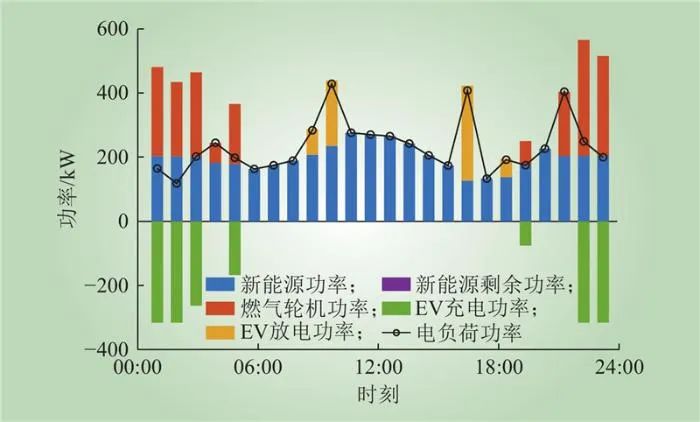
图14  VPP3供电设备最优运行计划

Fig.14  The optimal operation plan for VPP3

下层火电机组最优出清价格运行计划如图15所示。从图15中可以看出，火电机组主要在12:00—15:00等时段向上层电力市场出清。这是由于该时段属于气价高峰时段，燃气机组报价较高，进而火电机组分担更多的出清功率。

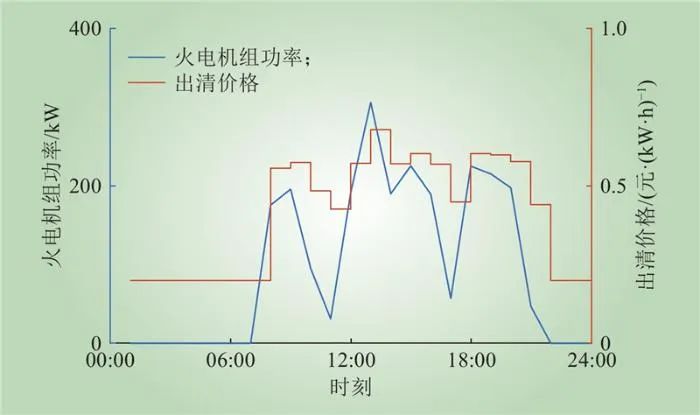
图15  火电机组最优运行计划

Fig.15  The optimal operation plan for thermal power unit

3.2.3  出清结果分析

在双层模型优化过程中，下层VPP集群和火电机组向上层电力市场报价，上层电力市场根据各VPP和火电机组的报价，分配负荷功率。此外，本文还考虑下层向上层电力市场提供的调峰服务，相同的方式向上层电力市场报最优调峰价格，上层电力市场根据各VPP和火电机组的报价情况，合理分配调峰需求。下层各VPP和火电机组的最优出清计划如图16所示。从图16中可以看出，火电机组功率的出清主要集中在08:00—18:00。分析表明，VPP1虽然风光发电功率较高，但由于VPP1自身带有负荷需求，导致VPP1会提升各设备报价，进而降低了VPP1分担的电力市场负荷功率；VPP2仅包含光伏发电设备，主要在10:00—17:00输出功率，导致VPP2更多地需要燃气机组和电储能设备分担上层电力市场负荷需求。由于燃气机组运行成本较高，与其他参与报价的VPP相比，在价格方面没有优势，因此，VPP2分担了最少的电力市场功率需求。此外，白天天然气价格较高，燃气机组没有了价格优势，火电机组分担了更多的出清功率。下层各个VPP和火电机组调峰功率的最优分配计划如图17~18所示，结合图16中可以看出，上层电力市场优先选择调峰价格低的设备参与调峰。由于VPP2在上层电力市场功率需求方面分担较少，VPP3燃气机组出力较少，因此可以有更多的燃气机组容量参与调峰，在调峰价格制定方面比其他VPP更具有优势；同时，由于调峰出现在中午时段，而该时段属于火电机组出清功率较高的时段，因此火电机组可以参与的容量较低。

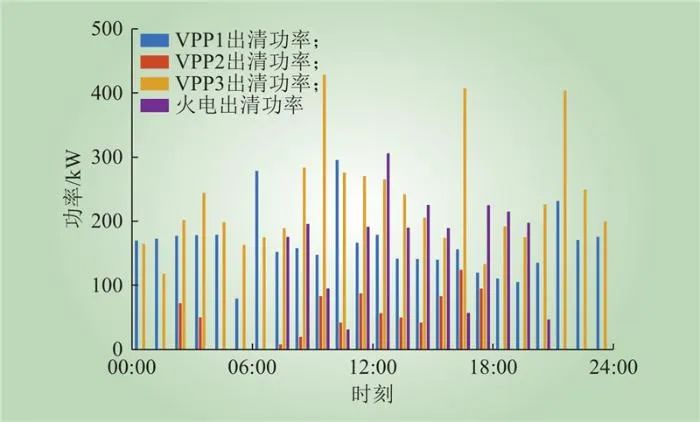
图16  最优出清计划

Fig.16  The optimal clearing plan

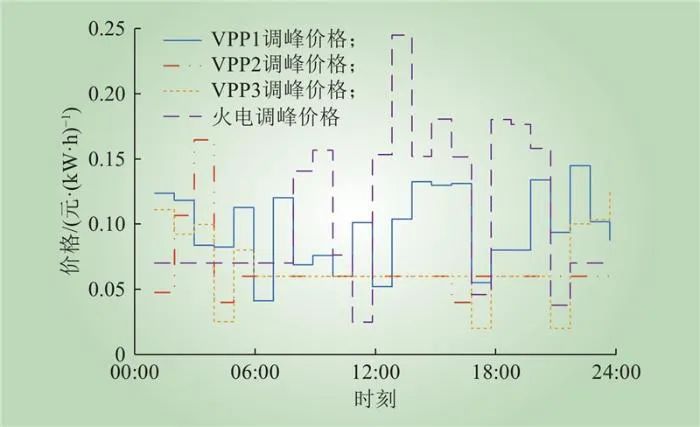
图17  最优调峰报价

Fig.17  The optimal peak shaving quotation

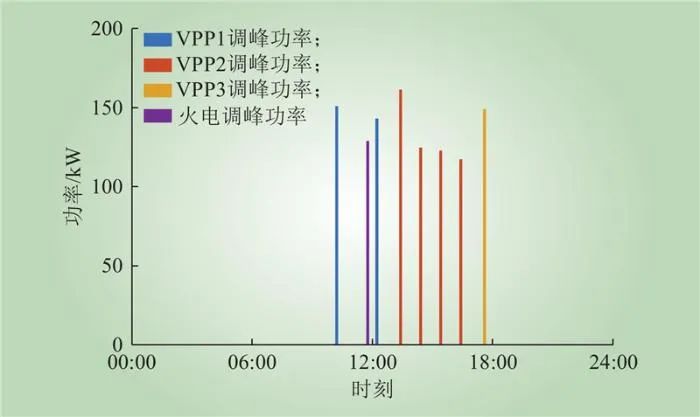
图18  调峰功率最优分配计划

Fig.18  The optimal peak shaving power allocation plan

为表明文中所提隐私算法的有效性，设计3个虚拟电厂进行实验。通过在具有隐私保护和无隐私保护两种情况下分别计算虚拟电厂出清功率，比较两者结果是否相等，从而验证隐私结算模型的可行性和正确性，结果如图19所示。从图19可以看出，本文方案解密之后的结果与明文下的VPP出清功率结果相同，证明本文提出模型和无隐私保护模型具有相同的精度，验证了提出模型的正确性。

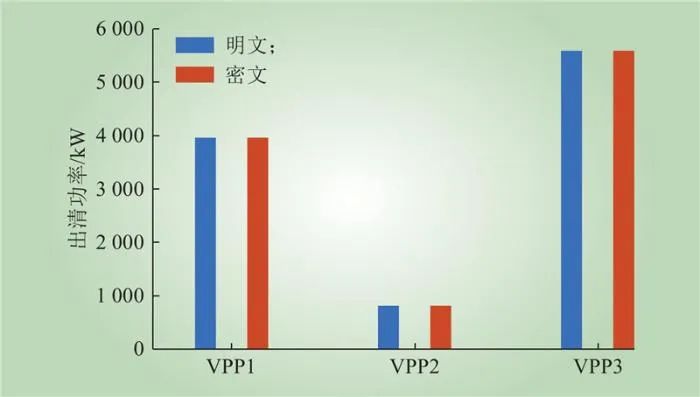
图19  VPP出清功率的正确性

Fig.19  The correctness of the VPP clearing power

3.3  不同价格申报机制对虚拟电厂运行的影响

为证明所提报价模型的有效性，本节设定4组对比算例进行分析。

场景1：采用分时电价作为下层VPP参与上层电力市场的出清价格，分时电价参见文献。

场景2：采用文献中VPP统一报价的方式参与上层电力市场，即不区分不同设备报价方式的差异。

场景3：采用所提差异化报价模型协调上下层利益关系，但不考虑碳交易、绿证交易和需求响应因素对下层VPP内部供电设备报价的影响；

场景4：采用所提差异化报价模型。

通过分析可知，与场景1相比，场景2中双层模型的联合运行指标、下层碳排放量、燃气机组功率分别降低了31.91%、19.97%和86.71%；同时场景2新能源机组的消纳功率提升了54.30%。

与场景2相比，场景3采用不同设备差异化报价机制降低了上层市场出清成本，降低幅度为24.89%；分析表明，场景2会通过提升报价的方式保证各设备出清收益，在出清需求不变的前提下，增大了上层市场出清成本。

相比于场景3，场景4考虑碳交易和绿证因素和需求响应因素后，使燃气机组功率和碳排放量分别提升了51.64%和3.67%。分析表明，所提价格申报机制提升了燃气机组的最优报价，提高了燃气机组参与市场的积极性，进而燃气机组功率和碳排放增大。

为验证所提报价机制在利益均衡分配、传统机组利润低等方面的优势，与场景2虚拟电厂统一报价机制相比，对两种不同报价机制下各供电设备收益、最优报价进行对比分析，结果如图20~21所示。其中。场景1为本文所提差异化报价机制；场景2为文献所提统一报价机制。从图20~21中可以看出，与场景2相比，场景1考虑差异化报价机制降低了新能源机组的报价，提升了燃气机组设备报价。同时，差异化报价机制提升了燃气机组出清收益，降低了传统机组（燃气机组）因收益过低进而退出电力市场的风险。

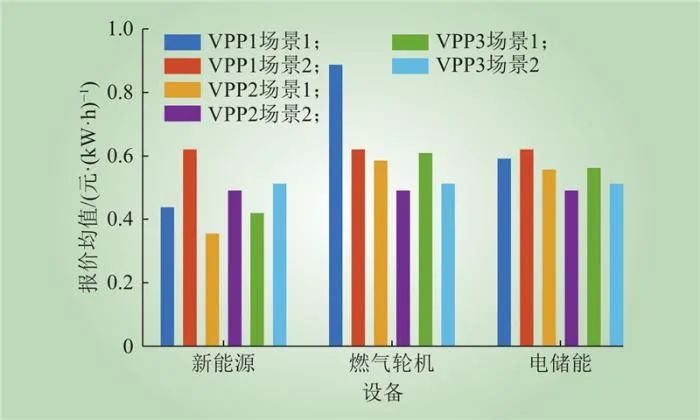
图20  不同场景下各设备报价均值

Fig.20  Average quotation value of each equipment in different scenarios

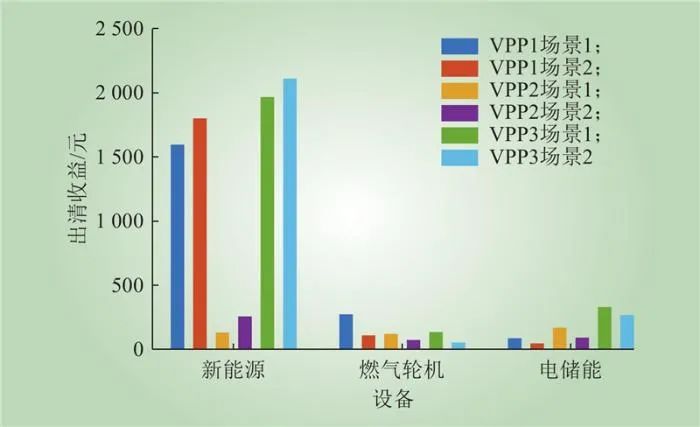
图21  不同场景下各设备出清收益

Fig.21  Clear revenue of each equipment under different scenarios

综上所述，所提差异化报价机制适当提升了传统机组市场竞争力，在实际应用中，虚拟电厂调度人员结合差异化报价机制，可以灵活调整传统机组报价，保证传统机组的收益、降低退市风险，维持形成的稳定运行。

3.4  虚拟电厂参数灵敏度分析

为分析不同因素对下层VPP和火电机组参与上层电力市场的影响，本节考虑VPP1需求响应和VPP3电动汽车等因素对系统运行影响分析。将VPP1电负荷需求响应占比分别调整为0%、10%、20%以及30%。

随着需求响应占比的增大，VPP1运行成本、碳排放量以及出清功率呈现逐步下降趋势，最大降低幅度分别为9.62%、70.73%以及10.17%；同时，VPP1负荷中断功率和调峰功率呈现逐步上升的趋势，VPP1负荷中断功率和调峰功率分别由场景1的0 kW增大到场景4的818.49 kW和443.14 kW。分析表明，电负荷需求响应特性改善了VPP1自身负荷用电计划，使负荷运行曲线更加贴合VPP1电源出力特性，增大对VPP1夜间燃气机组的出力，减少了天然气峰平时段燃气机组的功率，并通过中断部分负荷降低负荷高峰时段VPP1的供电压力，进而降低了VPP1运行成本和碳排放量。同时，由于VPP1自身电负荷优先对低成本电源的消耗，导致VPP1的最优报价不具备优势，进而降低VPP1的出清量。出清量的减少，代表VPP1可以空出更多的参与燃气机组容量参与上层电力市场调峰，调峰最优报价更具有优势，进而提升了VPP1承担的调峰需求。

将VPP3中接入电动汽车容量比例分别调整为50%、100%、150%以及200%。上述电动汽车初始充电需求为容量比例100%，在该基础上缩小比例或扩大比例。研究发现，随着VPP3电动汽车接入容量的增大，VPP3运行成本和碳排放量呈现逐步上升趋势，最大提升幅度分别为45.33%和45.83%；同时，VPP3出清功率和电动汽车放电功率呈现整体下降趋势，最大降低幅度分别为5.74%和33.12%。分析表明，电动汽车接入容量的增大，代表VPP3负荷需求变大，燃气机组增大出力维持电动汽车充电需求，进而VPP3运行成本和碳排放量增大；同时，VPP3各设备输出功率的变大，导致各设备向上层电力市场最优报价提升，进而VPP3出清功率呈现下降趋势；此外，在保证电动汽车供需平衡的前提下，电动汽车容量的增大代表电动汽车的放电能力降低，进而减少了电动汽车的放电功率。

3.5  所提模型可行性分析

本文所提模型要求VPP内各设备差异化报价，即一设备一价格。该方法解决了VPP统一定价下各设备的利益分配问题，可以直接按照设备最优报价和出清功率进行收益结算。同时，文中限定VPP内各设备向电力市场的报价次数上限，保证双层模型的求解时间满足工程要求。然而，随着电力市场内参与的VPP和设备的增多，所提双层模型的复杂程度会有所提升。为验证在VPP和设备增多的情况下所提双层模型的有效性，本文以所提3个VPP和11台设备为基础，对VPP和设备进行等比例扩大，所得结果如表1所示。

表1  双层模型的可行性分析

Table 1  Feasibility analysis of the bi-level model

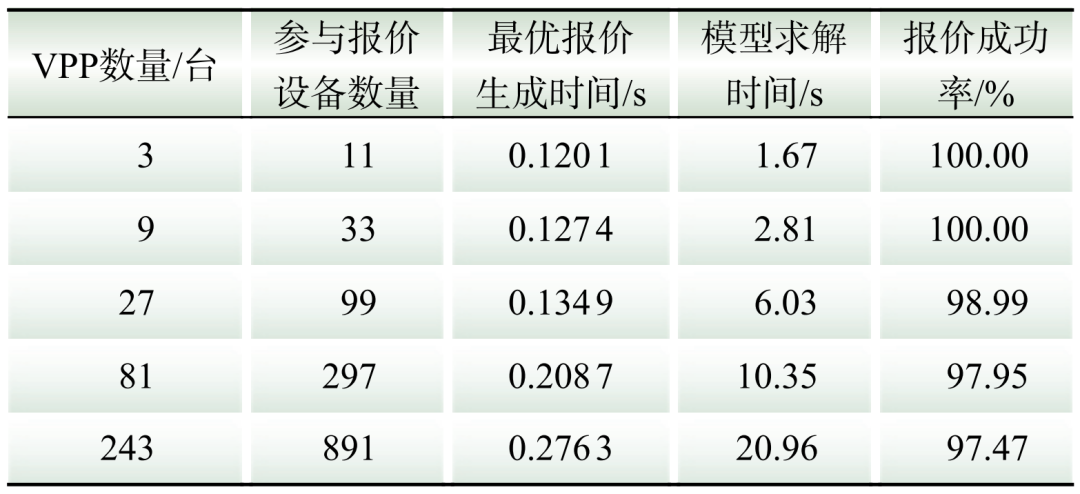
从表1可以看出，随着参与电力市场设备数量的增大，所提双层模型的求解时间和最优报价生成时间呈现上升趋势，最大提升幅度为56.53%和92.03%；报价成功率呈现下降的趋势，由100%降低至97.47%。分析表明，接入电力市场设备的增多，代表所提双层模型的复杂程度增大，进而时间提升；同时，由于文中设置了报价次数上限约束，参与报价设备的增多，导致价格竞争激烈，部分设备在报价次数限制内没有获得理想报价的会直接退出电力市场。

然而，当接入电力市场的设备数量达到891台时，双层模型的求解时间仅为20.96 s，最优报价生成时间为s。同时，本文所研究内容为VPP参与日前电力市场，因此，模型求解时间和设备最优报价生成时间能够满足实际工程要求。

04

结论

本文针对虚拟电厂内部供电设备通过报价方式参与电力市场优化的问题开展研究，提出一种考虑碳、绿证和需求响应因素的差异化报价机制，协调下层供电设备和上层市场之间的利益关系，通过CPLEX迭代求解双层模型，主要结论如下。

1）考虑碳交易和绿证因素的报价机制更好地协调了上下层之间的利益关系，同时降低了虚拟电厂碳排放水平。采用不同设备差异化定价的方式有效提升了传统机组的运行收益，降低了传统机组因利润过低退出电力市场的风险。

2）负荷需求响应占比提高会降低其运行成本和碳排放量，为下层VPP和火电机组的经济低碳运行带来积极影响；电动汽车容量增大提升了电动汽车参与上层市场的竞争力，整体提升了VPP的出清功率。

3）本文通过对所提双层模型可行性分析表明，所提模型在VPP和供电设备接入市场较多的情况下，在求解时间等方面仍能满足实际工程需求。

本文对虚拟电厂参与电能量-调峰联合市场的优化问题做了初步分析，后续研究将进一步考虑其他辅助服务市场以及电热、电氢等多能耦合市场。