储能变流器跟网/构网无扰切换控制技术研究

DOI：10.19799/j.cnki.2095-4239.2025.0642

本文亮点：1.基于跟网/构网控制方式下的稳态矢量的关系，构建了包含功角观测、坐标系旋转、PI调节器初始化等关键模块的跟网/构网无扰切换控制方法； 2.基于阻抗分析法，探究了两种控制模式下并网系统稳定性与电网短路比的关联机制，并提出在电网短路比动态变化时，可借助跟网/构网混合控制及无扰切换技术提升系统稳定性

摘 要 储能系统采用单一的跟网型控制(GFL)或构网型控制(GFM)时难以适配复杂多变的电网需求，本工作提出一种适用于储能变流器单元的跟网/构网无扰切换控制方法，实现构网控制与跟网控制随外部环境变化的平滑切换。基于跟网/构网控制方式下的稳态矢量的关系，构建了包含功角观测、坐标系旋转、PI调节器初始化等关键模块的跟网/构网无扰切换控制方法；基于阻抗分析法，探究了两种控制模式下并网系统稳定性与电网短路比的关联机制，并提出在电网短路比动态变化时，可借助跟网/构网混合控制及无扰切换技术来提升系统稳定性；基于储能系统的Matlab/Simulink仿真模型开展仿真测试及分析。仿真结果表明，本工作所提的切换方法可使并网储能变流器在跟网控制模式与构网控制模式之间无扰切换，且兼具优异的系统响应性与稳定性。本研究有助于提升高功率高频充放电的构网型储能设备的运行灵活性，使其具备在离网/并网、强电网/弱电网等复杂多变场景中的自适应能力，最大程度地保障系统的安全稳定运行。

关键词 储能变流器；跟网/构网无扰切换；宽频振荡；阻抗分析

随着全球对清洁能源的大力推广与应用，新能源发电在电力系统中的占比日益增加。在传统电力系统中，同步发电机凭借其强大的机电耦合特性(体现为固有转动惯量和阻尼特性)，在系统有功不平衡时，能够迅速通过转矩的变化来调整转速，进而维持系统频率的稳定，确保整个电网的可靠运行。然而，在当前高比例新能源接入的“双高”(高比例可再生能源、高比例电力电子设备)电网形势下，新能源发电固有的间歇性和波动性给电网带来了前所未有的冲击。

更为关键的是，大量新能源发电单元通过电力电子变流器并网，其控制方式与传统同步机有着本质区别，主流的新能源并网方式采用跟网型控制(grid-following control，GFL)。在该模式下，变流器被控制为一个受控电流源，其运行高度依赖于对电网电压相位(通常通过锁相环获取)的精确跟踪。研究表明，GFL变流器在提供系统惯性和阻尼支撑方面存在显著不足：其输出功率主要受电流指令控制，与电网频率之间缺乏固有的机电耦合关系，本质上无法像同步机那样在电网频率变化时通过释放或吸收动能来瞬时响应。这导致高比例新能源接入后，系统的等效惯量和阻尼水平显著下降，频率变化率增大，频率跌落深度增加，系统稳定性风险陡增，尤其是在弱电网

短路比(short-circuit ratio，SCR)较低

环境下。此外，GFL变流器的稳定性严重依赖于电网强度。在弱电网条件下，锁相环的动态性能与电网阻抗相互作用，极易引发次同步振荡或宽频振荡问题，且在电网发生严重故障导致电压深度跌落或相位突变时，锁相环可能失锁，甚至导致变流器脱网。这些都是现有大规模应用GFL变流器的核心痛点，严重制约新能源并网发电与送出能力。受系统稳定性约束，目前，青海、新疆等地区遭遇新能源并网和送出困境。

为了应对GFL变流器的上述缺陷，构网型控制(grid-forming control，GFM)技术近年来受到了广泛关注和研究。在该模式下，变流器被控制为一个受控电压源(或类似同步发电机)，其输出电压的幅值和相位由内部的控制算法自主生成，不依赖于锁相环信号进行同步。GFM变流器能够主动调节其输出以维持公共连接点的电压和频率，具备模拟同步机惯性和阻尼特性的能力，从而显著增强系统稳定性，特别是在弱电网或孤岛运行条件下。虚拟同步发电机(visual synchronous generator，VSG)控制是当前应用最广泛的GFM策略之一，其有功环直接生成电压相角(模拟同步机转子运动方程)，无功环生成电压幅值。

然而，构网型控制并非完美解决方案，其自身也存在挑战。研究表明，GFM变流器在电网正常运行(强电网)状态下，其有功功率跟踪精度和动态响应速度通常逊色于GFL变流器。更重要的是，在运行模式切换(如孤岛转并网、并网转孤岛)场景下，GFM面临严峻考验。GFM需要根据目标模式(并网或孤岛)调整其控制目标(如从频率/电压参考跟踪切换到自主设定或反之)和内部状态变量(如功角、虚拟惯量回路状态)，而固有的控制算法的切换过程往往不够平滑。这会导致切换瞬间并网点产生显著的电压和电流冲击，不仅威胁变流器自身及相连设备的安全，还可能引发暂态不稳定问题。如何实现运行模式间的平稳、无扰切换，已成为阻碍GFM技术大规模工程应用的关键瓶颈之一。

随着对电网稳定性和新能源利用效率要求的不断提高，单一的跟网型控制或构网型控制模式已难以满足复杂多变的电网需求。跟网/构网混合控制策略应运而生，其旨在融合两种模式的优点(GFL的精确功率跟踪能力与GFM的强电网支撑能力)。其中，切换型混合模式控制是一种极具前景的控制思路。其基本原理是根据电网状态(如SCR)在GFL和GFM之间进行动态切换：在强电网(高SCR)条件下采用跟网模式，充分发挥其优异的功率控制性能；在弱电网(低SCR)条件或需要主动支撑的场景下切换到构网模式，提供惯性和电压支撑能力。

在现有的切换型混合模式控制中：

（1）部分方法侧重于控制模式切换条件的判断，而未涉及具体的切换控制方法；由于电网运行工况复杂多变，受到负载变化、新能源发电间歇性、电网故障等多种因素的影响，电网阻抗处于动态变化之中，且谐波、电磁干扰等问题也会干扰检测结果的准确性。

（2）部分方法虽然提出了利用虚拟阻抗或反馈补偿的方法降低切换扰动，但是，所述虚拟阻抗的大小对控制特性有较大影响，需要仔细匹配，以避免负面作用的产生；所述反馈补偿存在一定动态调节时间，难以完全做到无扰切换。

为克服以上问题，本工作首先基于跟网/构网控制方式下的稳态矢量的关系，提出了一种适用于储能变流器单元的跟网/构网无扰切换控制方法，即：在构网模式下，利用第二锁相环观测功角，在跟网模式下，将常规端电压定向的dq坐标系旋转到内电势定向的xy坐标系，同时通过电压/功率外环初始化以及共用电流环确保切换过程的平稳性和无扰性。其次，基于阻抗分析法，分析了跟网/构网控制方式下，并网系统稳定性与电网短路比的关系，提出在电网短路比变化的条件下，利用跟网/构网无扰切换控制来提高系统稳定性。最后，通过仿真验证了所提切换方法的无扰特性以及在系统强度变化条件下提升系统稳定性的有效性。

1 控制模型

常规跟网型控制一般采用电压、电流双闭环矢量控制；构网型控制为了限制故障电流往往也增加电流环。因此，实现无扰控制的关键就是共用电流环，并实现电流给定的平滑过渡。1.1节综合两种控制结构给出了无扰切换控制的总体框图；1.2节则通过矢量分析，展示了如何通过选择适当的坐标系，实现两种情况下电流给定的一致；1.3节至1.8节进一步给出了各子模块的详细控制结构以及如何实现切换控制。

1.1总体结构

储能并网单元及其跟网/构网无扰切换控制系统如图1所示。其中，一次系统包括直流母线(直流电压Udc)、变流器、并网电抗器(电阻Rs、电感Ls)以及变压器等；二次控制系统包括旋转变换、功率计算、虚拟同步机、锁相环模块、电压调节器、功率调节器、电流调节器、反旋转变换、脉宽调制器、采样延迟(Z-1)等。控制系统首先采集并网系统端口三相交流电压Uabc和三相交流电流Iabc，经过各个控制模块的计算后，向变流器模块输出开关控制信号，用于实现交直流变换，并控制并网有功功率P和无功功率Q。

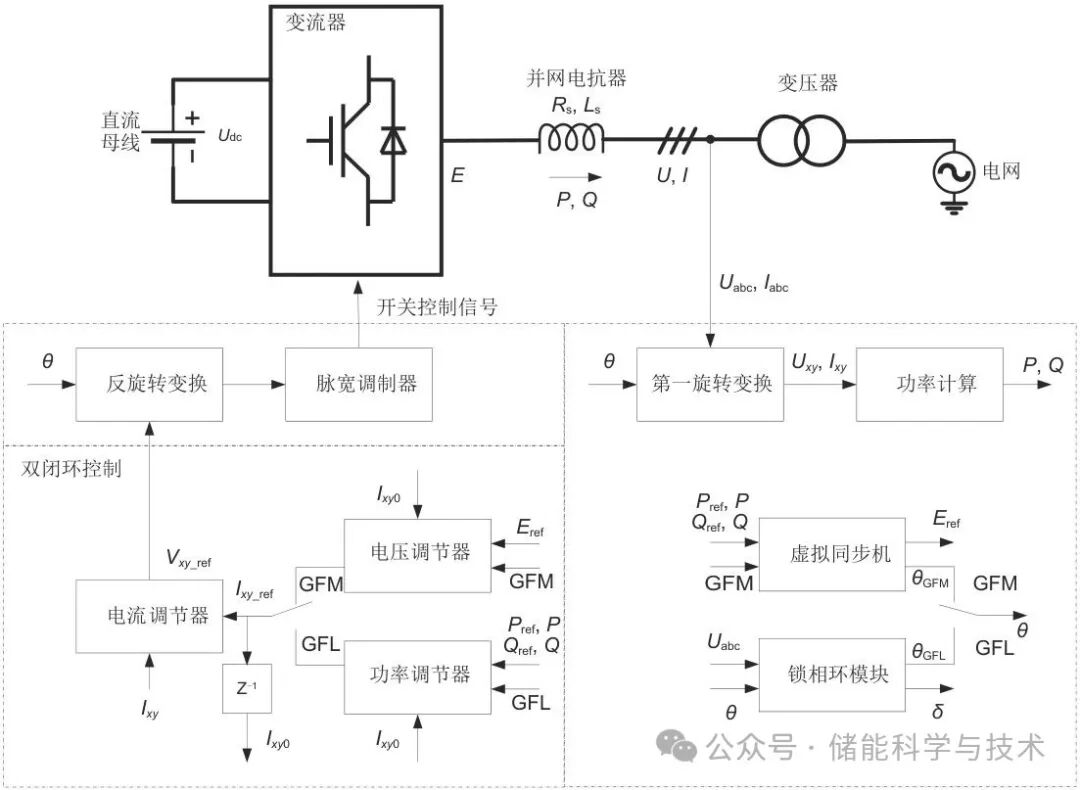
图 1   储能并网单元及其跟网/构网无扰切换控制系统

1.2矢量关系

无扰控制的关键是实现电流环给定的平滑过渡，也就是控制系统内部各状态变量的平滑过渡，本节通过分析矢量关系，推导出具体实现方法。

在电磁暂态研究范围内，储能系统直流母线电压波动很小，因此不妨令直流电压为额定值，同时忽略高频开关过程，容易得到储能系统的稳态模型：

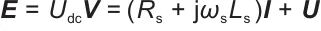
(1)

式中，

为等效内电势矢量，

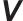
为变流器控制电压矢量，

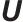
为并网端电压矢量，

为并网电流矢量，

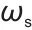
为电网角频率。

式(1)的矢量关系如图2所示。其中dq坐标系为常规旋转坐标系，其d轴与端电压矢量同向，xy坐标系为内电势旋转坐标系，其x轴与内电势矢量同向，二者夹角δ即为虚拟功角。

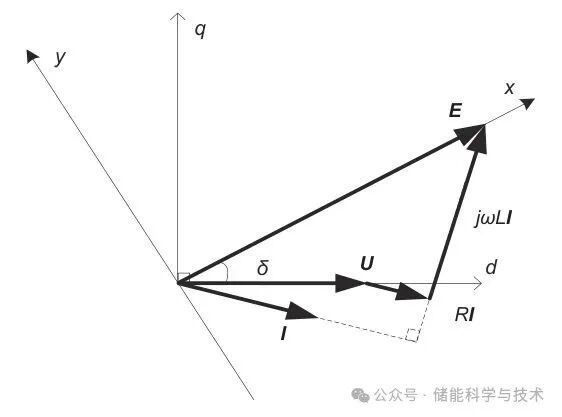
图 2   系统稳态矢量关系

由于常规跟网控制不观测功角，而常规构网控制不定位端电压，因此在切换时存在较大扰动。针对该问题，本工作提出在构网模式下，利用第二锁相环观测功角，在跟网模式下，将常规端电压定向的dq坐标系旋转到内电势定向的xy坐标系，实现了跟网与构网控制内部变量的一致性；同时通过电压/功率外环初始化以及共用电流环确保切换过程的平稳性和无扰性。

首先通过第一旋转变换将三相交流电压Uabc和三相交流电流Iabc变换为xy坐标系下的电压Uxy、电流Ixy，并计算得到xy坐标系的功率P、Q：

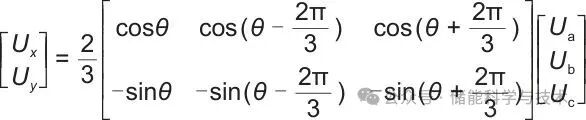
(2)

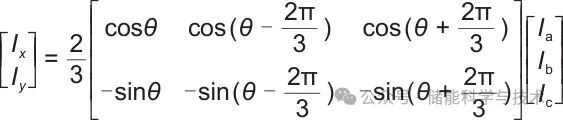
(3)

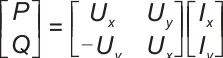
(4)

式中，

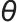
为系统旋转角，在构网(GFM)模式下

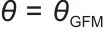
，在跟网(GFL)模式下

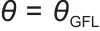
1.3构网控制

本工作的构网控制采用虚拟同步机(VSG)控制，即在构网控制(GFM=1，GFL=0)模式下，通过数学公式与控制模拟同步发电机的响应特性。具体的，根据有功功率偏差生成内电势角度

，根据无功功率偏差生成内电势参考值

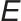
，如图3所示。

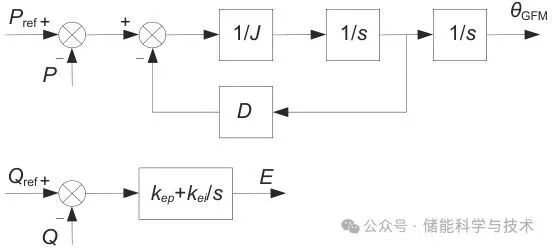
图 3   虚拟同步机控制框图

图3中，下标ref表示参考值，

为系统旋转角度，

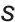
为微分算子，

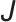
为等效惯量，

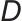
为等效阻尼系数，

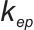
为比例系数，

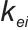
为积分系数。

1.4锁相环模块

本工作对锁相环模块进行了改进，可以同时得到系统旋转角度

以及构网控制功角

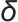
，如图4所示。

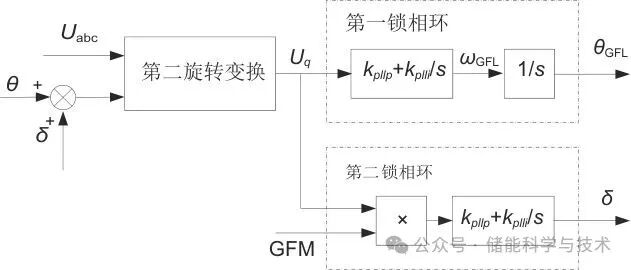
图 4   锁相环模块控制框图

具体的，先通过第二旋转变换计算dq轴电压：

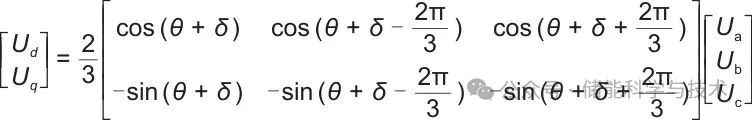
(5)

然后将q轴电压Uq送入第一锁相环进行计算：

(6)

式中，

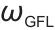
为系统角频率，

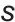
为微分算子，

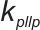
为锁相环比例系数，

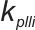
为锁相环积分系数。

同时将q轴电压Uq送入第二锁相环进行计算：

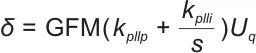
(7)

在跟网控制模式下GFM=0，在构网控制模式下GFM=1。需要注意的是，第二锁相环只在构网模式下有效，在跟网模式下则保持输出不变。这是因为在跟网模式下，功率与坐标系旋转角度解耦，无法直接观测构网控制功角。因此，为了保证切换的平稳性，在跟网模式下需要锁定构网控制功角

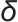
，且在由跟网向构网切换时应回到上一次切换的工作点(功率设定值)。

1.5电压调节器

双闭环控制包含了电压调节器、功率调节器以及电流调节器，如图5所示。

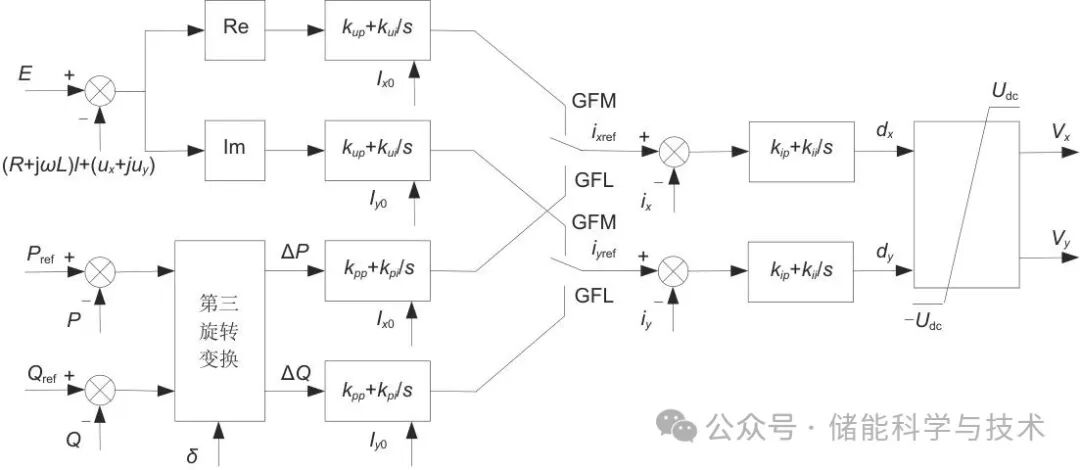
图 5   双闭环控制框图

在构网模式下，电压调节器根据虚拟同步机模块输出的内电势参考值E计算得到电流参考值ixyref，计算公式如下：

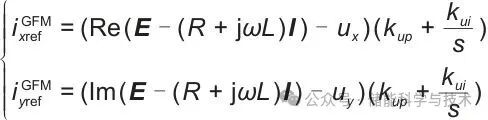
(8)

式中，Re( )为取复数的实部函数，Im( )为取复数的虚部函数，E为内电势矢量，I为并网电流矢量，

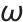
为同步角频率，

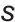
为微分算子，

为电压环比例系数，

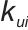
为电压环积分系数。

在跟网/构网控制模式切换时，须对电压调节器内部积分器状态变量进行更新，更新的初值为切换时刻的电流给定值。

1.6功率调节器

在跟网模式下，首先通过第三旋转变换(图5)将功率偏差值转换到xy轴坐标系，然后通过PI调节器计算得到电流参考值ixyref，计算公式如下：

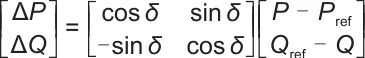
(9)

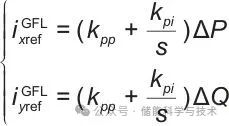
(10)

式中，

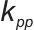
为功率环比例系数，

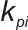
为功率环积分系数。

在跟网/构网控制模式切换时，将对电压调节器内部积分器状态变量进行更新，更新的初值为切换时刻的电流给定值。

1.7电流调节器

在构网模式下，选取电压调节器的输出作为电流参考值ixyref；在跟网模式下，选取功率调节器的输出作为电流参考值ixyref，然后通过PI调节器计算得到占空比dxy，计算公式如下：

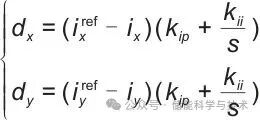
(11)

式中，

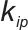
为电流环比例系数，

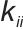
为电流环积分系数。

然后通过控制电压限幅环节，得到阀侧控制电压Vxy，计算公式如下：

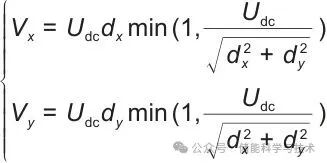
(12)

式中，Udc为直流母线电压，min( )为取最小值函数。

1.8反旋转变换与脉宽调制器

反旋转变换模块将Vxy转换成三相电压量Vabc：

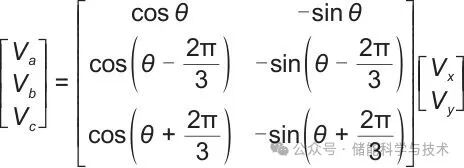
(13)

然后将Vabc与三角波进行比较，得到变流器的开关控制信号，该过程为常规变流器的基本步骤，不再赘述。

2 仿真验证

2.1切换控制仿真

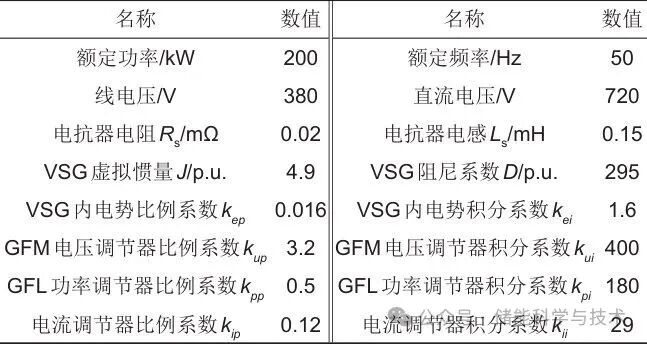
基于图6所示的RT-LAB半实物仿真平台，构建图1所示系统的仿真模型，主要参数如表1所示。

图 6   RT-LAB半实物仿真平台

表1   仿真系统参数

在不同SCR条件下，以2 s为周期，在跟网控制与构网控制之间进行切换，仿真结果如图7所示，其中下标x表示定位到内电势方向的x轴，下标y表示与x轴垂直的方向，可以看到在切换时，系统输出功率与电压电流平稳无扰动，验证了所提方法的有效性；且SCR主要影响启动过程，对切换过程基本没有影响。

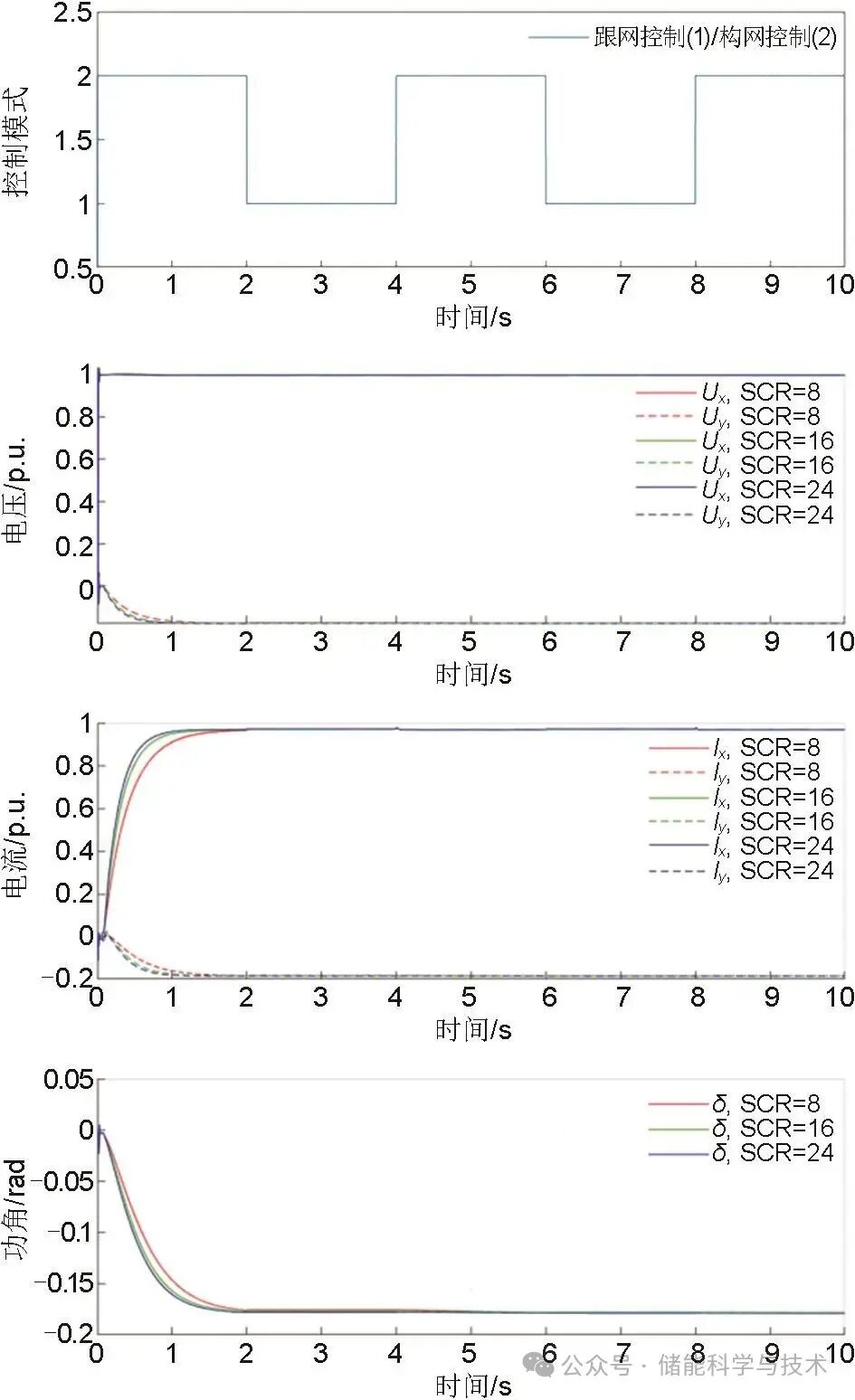
图 7   跟网/构网切换控制仿真结果

2.2振荡抑制仿真

构网型储能外特性为电压源，当多个构网型储能单元近距离并联运行时，系统内有多个存在微小差异的“电压源”，各“电压源”并列时易发生振荡。为验证该控制方法在多机并列运行时的响应能力及稳定性，本工作构建了双机仿真系统，研究混合控制对提高系统并网性能的作用，如图8所示。每个储能单元都具备GFL/GFM双模式控制系统。为研究混合控制对提高系统并网性能的作用，设计如下场景：

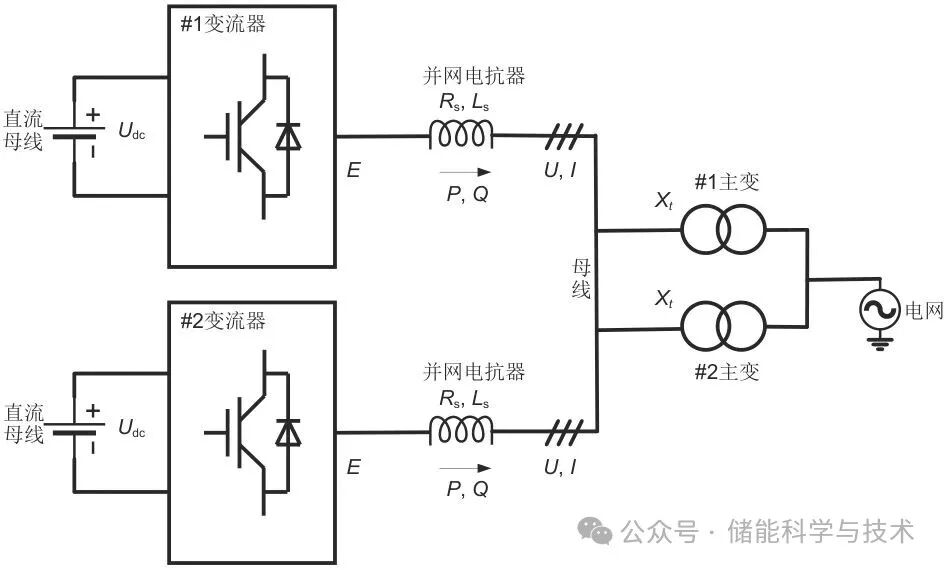
图 8   双机仿真系统

（1）系统运行方式变化导致并网点系统强度变弱；

（2）原有控制方式不适应弱电网条件，产生振荡；

（3）部分机组由GFL切换至GFM控制；

（4）系统振荡得到有效抑制。

系统强度一般采用短路比定义，在图8所示系统中，将两台储能系统聚合考虑：

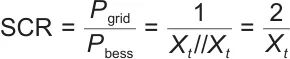
(14)

式中，

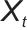
为变压器漏感电抗，//表示并联。两台主变若有一台故障或检修，则系统强度减半(例如，SCR由18降低到9)。

首先在频域下，测量储能变流器在不同工作模式下的端口阻抗，其频谱特性图如图9所示。根据阻抗分析法，由图9可知：

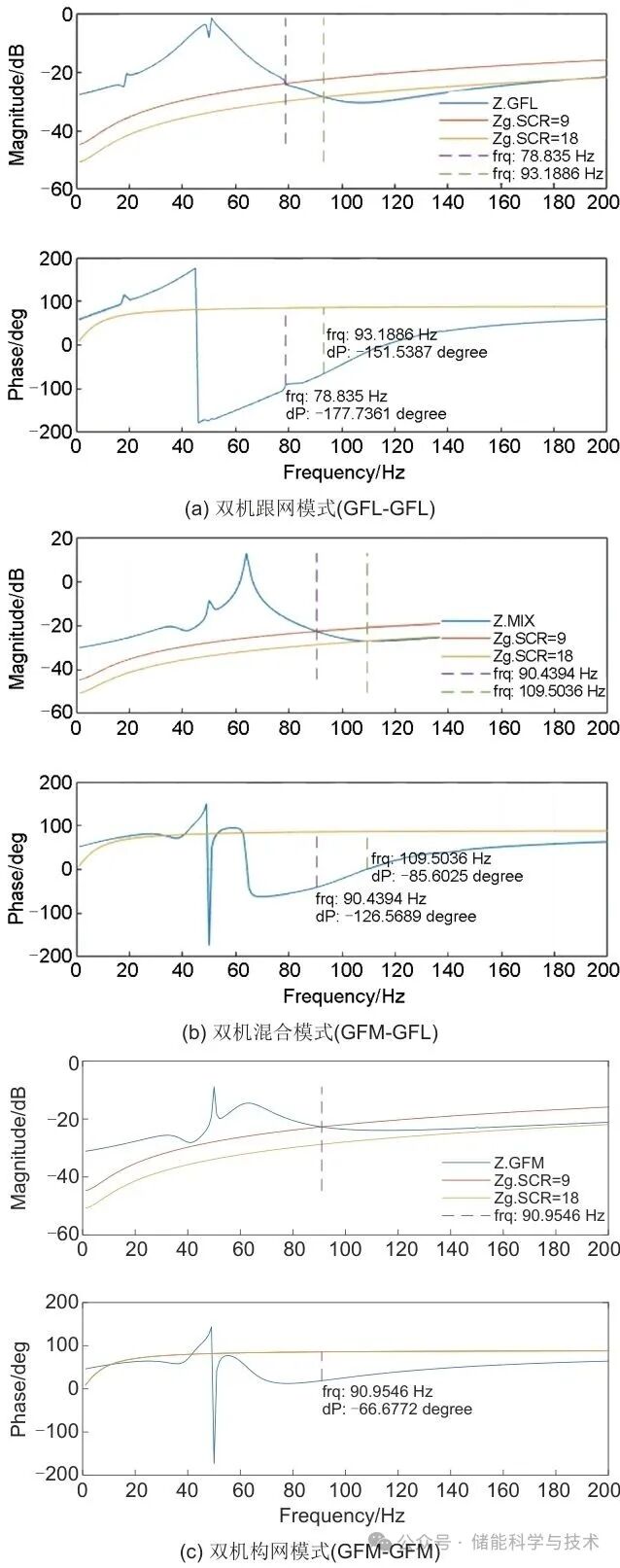
图 9   阻抗扫描结果

（1）对于双机跟网模式(GFL-GFL)，随着系统强度的降低，SCR减小，系统容易出现振荡。在SCR=18(双主变)时，幅频曲线交点在93.19 Hz，相位裕度约为28.5°；而在SCR=9(单主变)时，幅频曲线交点在79 Hz，相位裕度约为2.3°，系统接近临界稳定状态。

（2）对于双机混合模式(GFM-GFL)和双机构网模式(GFM-GFM)，系统稳定性较强，不存在不稳定频率点，且双机构网模式相位裕度更大。

其次，在时域下，开展暂态波动仿真验证：设置双机仿真系统在t=0.05 s时，启动变流器，实现双机启动；在t=0.2 s时，改变系统输出有功功率和无功功率，令Pref=1 p.u.，Qref=0.1 p.u.；在t=2 s时，设置一台储能系统退出运行。仿真结果如图10、图11所示。

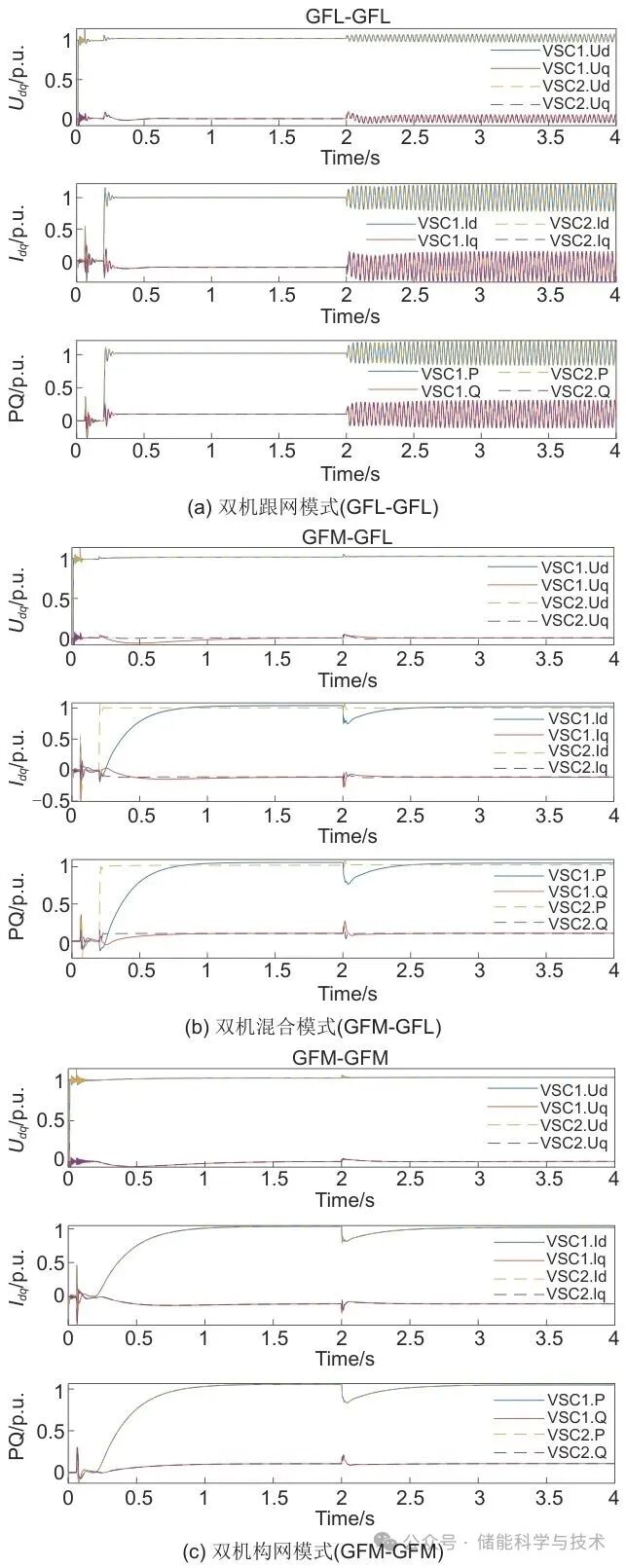
图 10   时域仿真结果

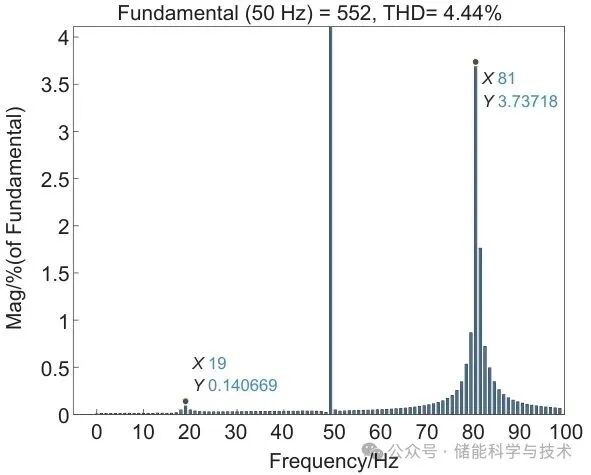
图 11   GFL模式并网电流FFT分析结果

从图10中可以看到：

（1）在双机跟网模式(GFL-GFL)下，系统变弱后产生振荡，FFT结果(图11)显示振荡频率为81 Hz，与阻抗分析结果基本一致。

（2）在双机构网模式(GFM-GFM)以及双机混合模式(GFM-GFL)下，系统稳定无振荡。且混合模式时，VSC1(GFL模式)的动态响应较VSC2(GFM模式)快，因此混合模式的整体响应较双机构网模式快，一台主变退出造成的功率扰动也更小。

最后，为充分利用两种模式各自的优点，本工作在双机跟网控制模式下开展振荡抑制仿真，仿真中为更加精确地控制传输功率，在t=2.0 s前采用双机跟网模式(GFL-GFL)，系统运行中设置远端电网暂态波动，储能系统在检测到振荡后(t=2.1 s)，将部分机组(VSC2)切换成构网模式，以抑制振荡，平滑系统电压及频率，如图12所示。

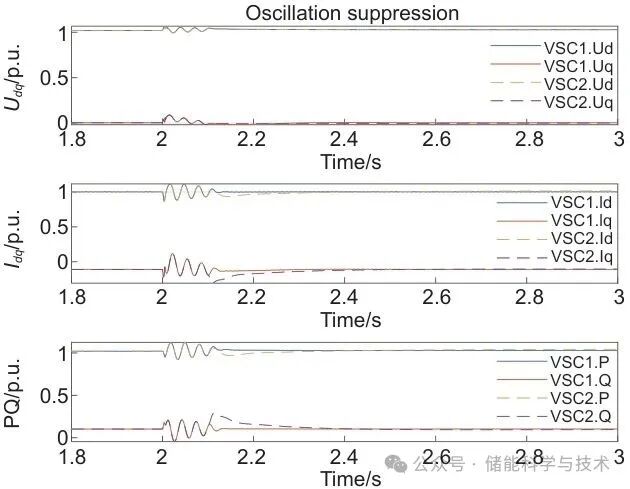
图 12   基于模式切换的振荡抑制

3 结论

随着可再生能源并网容量的增加，新能源与储能变流器需要具备更强的电网支撑能力。为适应不同的电网条件，基于跟网/构网控制方式下的稳态矢量的关系，本研究提出了一种适用于储能变流器单元的跟网/构网无扰切换控制方法，给出了详细的控制系统结构，并搭建单机、双机储能系统RT-LAB仿真平台，开展模式切换及振荡抑制仿真测试，并给出不同模式下的阻抗分析，仿真及分析结果表明：

（1）所提方法能够实现并网储能变流器在跟网(GFL)模式与构网(GFM)模式之间无扰切换。

（2）阻抗分析结果表明，GFL模式通常具有较强的指令跟踪与响应能力，适用于强电网；而GFM模式通常具有较强的稳定性，适用于弱电网。

（3）在电网强度发生变化(例如一台储能设备发生故障而退出或检修)时，系统容易发生宽频振荡，而基于跟网/构网混合及在线切换的控制策略，能够有效地兼顾系统响应特性与稳定性的要求，具有较强的实用价值。

第一作者：李功强（1977—），男，本科，高级工程师，研究方向为新能源、储能及水电管理