基于不完全量测数据的配电网状态估计方法

“双碳”战略的实施加速了分布式能源在配电网中的接入，导致配电网运行特性发生深刻变化。同时，分布式能源的不确定性削弱了配电网的实时可观性，难以精准监测其运行状态，由此引发的过载、过压和供电质量下降等问题已严重威胁配电网的安全性和稳定性。传统配电网状态估计方法依赖全面、精确的量测数据，然而，实际运行中数据不完整的现象普遍存在，使得传统方法难以满足估计精度和适应性的要求。在此背景下，亟须开发适用于不完全量测数据环境的高效状态估计方法，以保障配电网的稳定性与供电可靠性。

《中国电力》2025年第5期刊发了李鹏等撰写的《基于不完全量测数据的配电网状态估计方法》一文。文章提出一种基于贝叶斯优化CNN-LSTM的配电网状态估计方法。首先，基于有限的量测数据，采用生成对抗网络（generative adversarial networks，GAN）生成CNN-LSTM离线训练所需样本。然后，利用CNN提取关键特征，降低计算复杂度；利用LSTM处理时间序列数据，捕捉配电网的动态变化；利用贝叶斯优化自动调整超参数，提高模型精度和鲁棒性。最后，将实时量测数据导入训练完成的模型，用以预测配电网各节点的电压幅值与相角，并在IEEE 33和IEEE 123节点网络进行测试验证所提方法的有效性。实验表明，该方法在数据不完整和噪声干扰下表现出更高的适应性和精度，有效弥补了传统深度学习方法的不足。

摘要

随着分布式能源的大规模接入，传统配电网的运行特性发生显著变化，导致负荷分散、实时可观性差和数据不完整等问题，严重影响了配电网的状态监测和运行优化。对此，提出了一种基于不完全实时量测数据的贝叶斯优化卷积神经网络（convolutional neural networks，CNN）与长短期记忆网络（long short-term memory，LSTM）结合的配电网状态估计方法。该方法分为离线学习和在线状态估计2个阶段。离线学习部分，利用生成对抗网络生成所需样本，以训练CNN-LSTM模型，并采用贝叶斯优化算法调整超参数，从而提升算法的准确性。在线状态估计部分，基于不完全的配电网实时数据和训练完成的CNN-LSTM模型进行在线状态估计。最后，算例基于IEEE 33和IEEE 123网络进行仿真分析，验证了所提状态估计方法的有效性和准确性。

01

方法框架

传统状态估计算法通常基于冗余的配电网实时量测数据，并利用WLS算法估计当前运行状态，但在实时量测数据不足的情况下应用受限，难以保证估计精度。为解决上述问题，本文所提状态估计方法利用贝叶斯优化构建代理模型，在不完全量测的情况下预测最优参数设置，并通过不断更新和优化模型参数，提升模型对缺失数据的容错能力。同时，CNN具备强大的特征提取能力，LSTM则擅长处理时间序列数据，二者互补，可有效捕捉配电网运行状态的动态变化。结合贝叶斯优化和CNN-LSTM的优势，该模型能够进行在线学习和自适应调整，逐步提高配电网状态的估计精度。整体建模思路如图1所示，包含3个阶段，阶段1通过数据预处理，转换原始数据并填补缺失，为CNN-LSTM训练准备充足的数据样本；阶段2进行CNN-LSTM模型的训练，以满足状态估计的精度要求；阶段3将实时数据输入训练好的CNN-LSTM模型，通过前向计算得到状态估计结果。

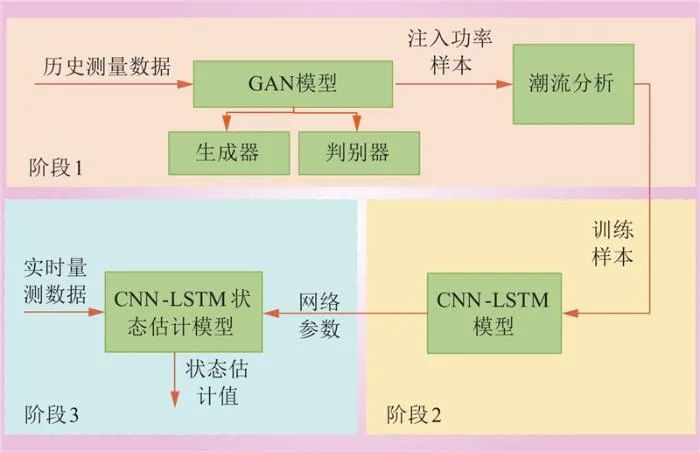
图1  总体建模思路

Fig.1  Overall modeling approach

1）阶段1。该部分由GAN模型和潮流分析校验组成。首先，通过历史测量数据训练GAN模型，其中生成器生成注入功率样本，判别器区分生成样本和真实数据。随后，进行潮流校验以确保测量样本的准确性。

2）阶段2。该部分利用GAN生成的测量-状态数据进行CNN-LSTM训练，在不完全量测情况下，采用贝叶斯优化算法预测最优参数设置。

3）阶段3。该部分将训练完成的CNN-LSTM模型应用于在线状态估计。通过向CNN-LSTM模型输入实时测量数据，可快速获得准确的状态估计结果。

02

基于GAN的测量数据增强

为解决历史测量数据不足的问题，本文提出了一种基于GAN模型的配电网测量数据生成方法。由于用户负荷变化，电网测量数据实时波动，导致数据分布呈现多个峰值而非单一正态分布。对此，本文采用GAN模型，通过神经网络作为函数逼近器，直接估计概率分布参数，从而生成有效的测量数据。GAN模型由生成器和判别器构成，通过对抗博弈过程达到纳什均衡，其目标是最小化生成器和判别器的损失函数，使生成样本逼近真实样本。

判别器旨在最大化对真实样本的判别概率，同时最小化对生成样本的判别概率，其目标函数L为

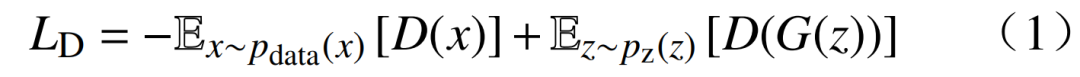
式中：

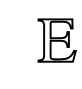
为期望的分布；x为真实样本；z为随机噪声；D(x)为判别器对输入的真实样本x判定为真的概率；G(z)为生成样本；D(G(z))是判别器对生成样本G(z)的概率估计；pdata(x)为真实数据的分布；p(z)为噪声的分布。

生成器的目标为最小化判别器对生成样本的概率估计，其目标函数L为

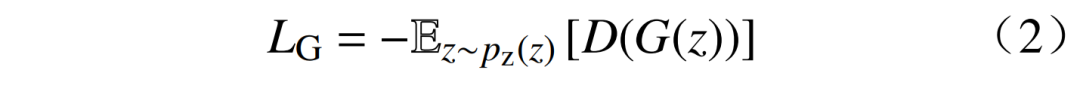
博弈过程的目标函数为

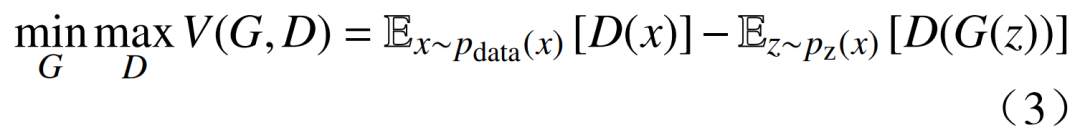
尽管GAN模型在数据生成方面表现出色，但常遇到训练不稳定和梯度消失等问题。为此，引入目标函数Wasserstein距离衡量博弈过程，显著提升训练稳定性。Wasserstein距离是一种衡量2个概率分布距离的度量，其定义为

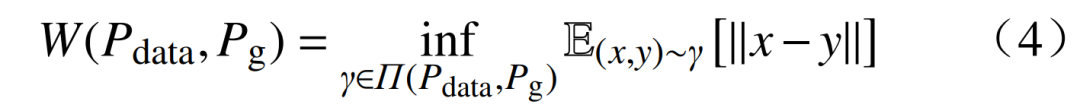
式中：W(P,P)为真实数据Pdata与生成数据Pg的分布相似度函数；inf为下确界的运算符；γ为联合分布；Π(P,P)为所有联合分布集合；||x−y||为样本x与样本y之间的欧氏距离。

为简化Wasserstein距离的计算，可将复杂的联合分布优化转化为对Lipschitz函数的优化，即

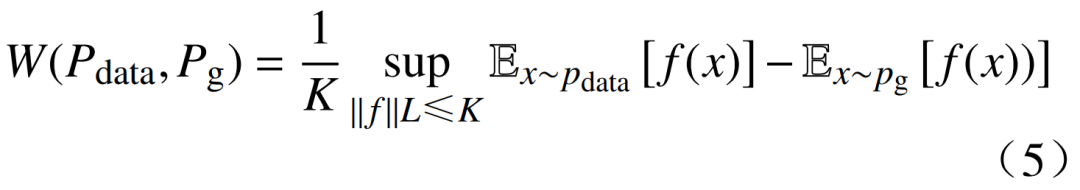
式中：1/K为归一化因子；sup为上确界的运算符，用于找到f(x)中的最大值；||f||L⩽K为一个约束条件，限制函数f(x)满足Lipschitz连续。

训练完成后，利用生成器产生高质量节点注入功率数据。随后，通过潮流计算，生成用于神经网络模型训练的样本数据集。最后，为验证测量-状态数据作为模型训练集的适用性，进行潮流校验，以增强模型训练的效果和可靠度。

03

基于贝叶斯优化CNN-LSTM的状态估计方法

3.1  CNN-LSTM网络构建

神经网络以其高容错性、强自适应性和海量数据的并行处理能力著称，其能高效处理非凸函数，实现最小正则化和成本松弛的目标。将其与配电网状态估计相结合，可为大数据时代的新型配电网提供强有力的技术支撑。

CNN能够从不完全的量测数据中提取出关键特征，有效降低计算复杂性。标准的CNN架构通常包括输入层、卷积层、池化层和全连接层等，依次用于数据处理、特征提取、降维和最终分类或回归任务，结构如图2所示。

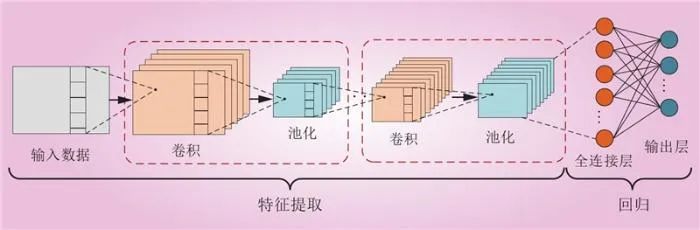
图2  卷积神经网络结构

Fig.2  Convolutional neural networks structure

为应对不完全量测数据中的特征缺失，CNN通过前向传播和反向传播提取关键特征，提升数据的有效性。前向传播中，不完全量测数据逐层传递并处理，提取的特征用于捕捉配电网的状态变化；反向传播则通过调整权重优化网络性能，提升状态估计精度。

尽管CNN在处理不完全量测数据时静态特征提取方面表现优异，但配电网状态估计还需要考虑时间序列的动态变化。为捕捉这些时间依赖关系，本文引入LSTM模型，以弥补CNN在处理时间序列数据方面的不足。LSTM模型由遗忘门fa、输入门ia和输出门oa构成，其中，a为循环次数。通过3个门的交互作用，神经元能够选择性地保留、遗忘、输入和输出信息，从而捕捉长时间依赖关系，有效解决循环神经网络中的梯度消失和梯度爆炸问题。

CNN-LSTM组合模型的结构如图3所示。整个模型首先通过CNN模块的卷积层和池化层对输入数据进行特征提取。然后，提取的特征通过展平层转换为一维向量。接着，数据经过重复向量层调整维度后进入LSTM模块，LSTM层负责捕捉时序信息。最后，通过丢弃层防止过拟合，并通过全连接层整合特征，最终在输出层生成预测结果。

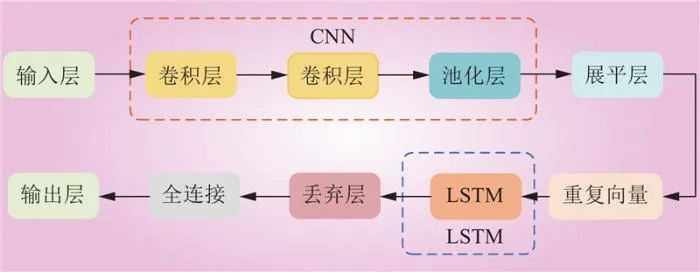
图3  CNN-LSTM组合模型结构

Fig.3  CNN-LSTM combined model structure

3.2  基于Adam算法的CNN-LSTM训练

为提升状态估计模型的准确度，本文选用适应性矩估计（adaptive moment estimation，Adam）优化算法来训练模型。Adam算法结合了动量法和自适应学习率的思想，能够有效应对非凸优化问题，加速模型收敛，进而提高状态估计模型的准确性，具体步骤如下所示。

1）初始化学习率rate、一阶矩估计的指数衰减率β1、二阶矩估计的指数衰减率β2和用于数值稳定性的常数η，参数η是一个很小的接近于0的正数。

2）在每个训练批次中计算损失函数关于参数的梯度。

3）计算一阶矩估计mt和二阶矩估计vt的衰减平均值，即

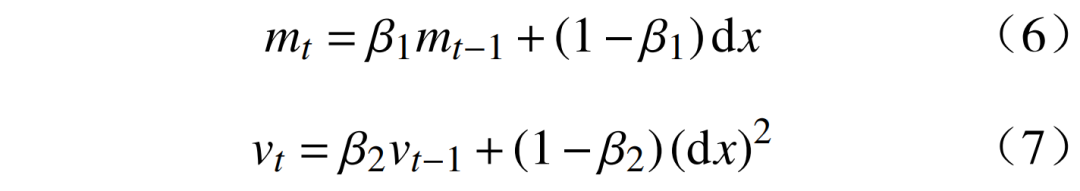
式中：t为循环次数；dx为梯度。

4）通过计算偏差修正一阶和二阶矩估计，以减轻初始化时将它们设置为零向量而产生的偏差，即

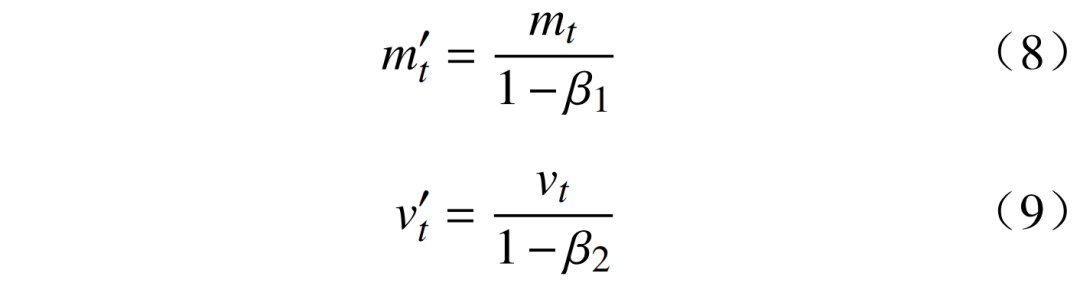
式中：分别为修正后的一阶矩估计和二阶矩估计。

5）使用修正后的值更新参数，即

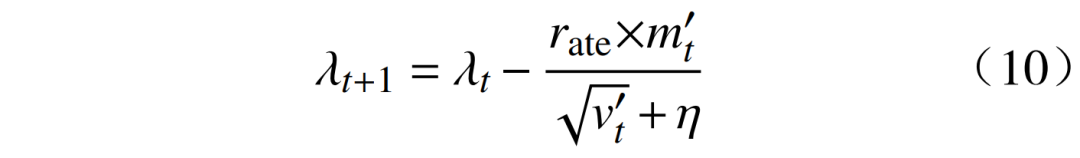
式中：λt、λt+1为参数。

6）重复上述过程，直到达到预设的停止条件。

3.3  基于贝叶斯算法的超参数优化

神经网络的参数主要分为模型参数和超参数2类。模型参数在训练过程中自动调整，无须人工干预。CNN-LSTM模型的性能高度依赖于超参数的选择。然而，超参数空间复杂且搜索过程极为耗时，尤其是在CNN-LSTM这样的深度网络中。此外，由于超参数与模型性能间缺乏直接的数学关系，传统基于梯度的优化方法难以有效应用。

针对上述问题，本文引入贝叶斯优化算法，通过构建目标函数的代理模型，利用已评估的少量超参数点进行拟合和预测，从而显著减少训练次数。相较于随机搜索等传统方法，贝叶斯优化算法能够更加高效地探索超参数空间，显著缩短计算时间。此外，其基于观测值的推断机制无需显式梯度信息，可有效处理目标函数的不可导性，详细过程如下所示。

1）确定循环次数t。

2）基于当前神经网络的超参数集σt和观测误差εt，通过优化特定函数来选定一个新的点进行评估，得到对应于σt的网络性能观测值bt。每次迭代结束时，将新的观测(σt, bt)加入到现有数据集合D1:t={D1:t–1,(σt, bt)}中，并利用此数据更新模型。

3）重复进行此过程，直到达到预设的循环次数t。

整个流程是一个迭代过程，通过不断地评估、更新和优化，最终得到一个在给定任务上表现最佳的CNN-LSTM模型。基于贝叶斯优化的CNN-LSTM模型优化流程如图4所示。

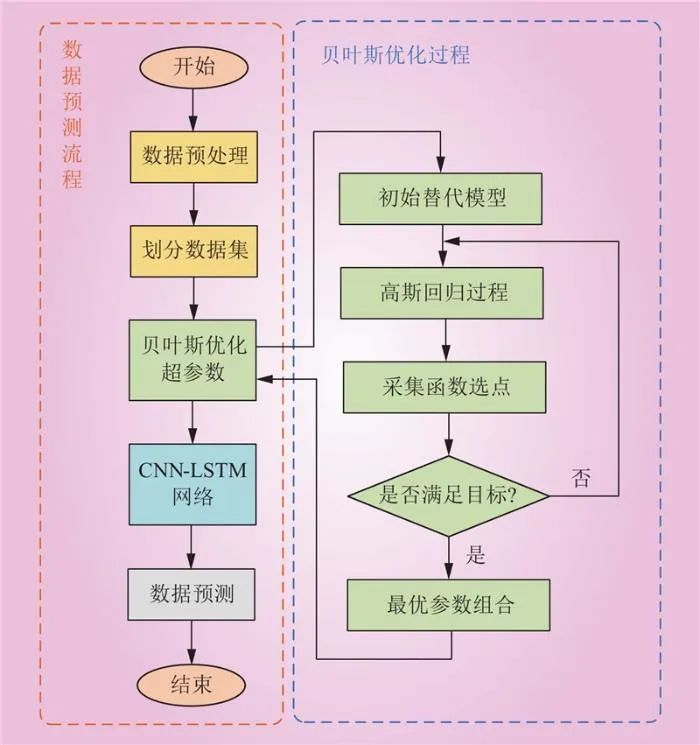
图4  基于贝叶斯优化的CNN-LSTM模型优化流程

Fig.4  CNN-LSTM model optimization process based on Bayesian optimization

04

算例分析

本文在改进的IEEE 33节点和IEEE 123节点配电网上进行算例分析。运用Matpower 7.0计算潮流，生成模型训练时所需样本并进行潮流校验。此外，CNN-LSTM模型的训练通过Matlab内置的深度学习工具箱完成。

4.1  IEEE 33节点算例分析

在改进的IEEE33节点算例中，节点1、5、9、13、19、22、26和30处安装实时量测装置，如图5所示。

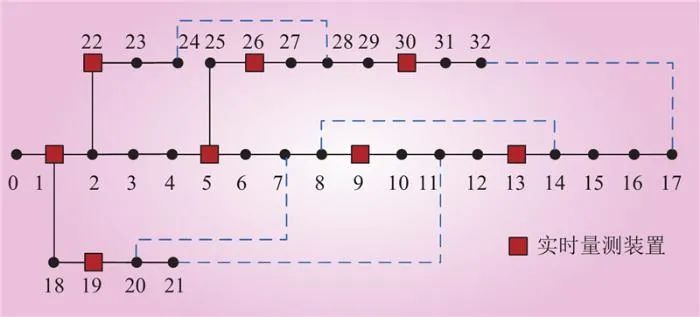
图5  IEEE 33节点配电网测量配置

Fig.5  Measurement configuration of the IEEE 33-node distribution network

利用爱尔兰地区2019年1—3月共3个月的实际运行数据进行分析，其中每30 min的数据构成一个样本断面，总共形成个断面。随后，将数据随机分配至IEEE 33节点网络。选取前个断面数据作为训练集，后320个作为测试集。接着，利用训练集训练GAN，生成个有功、无功负荷样本，并通过Matpower进行潮流计算，以产生测量-状态样本。同时，为避免不同量纲的影响，对数据进行了归一化处理，即

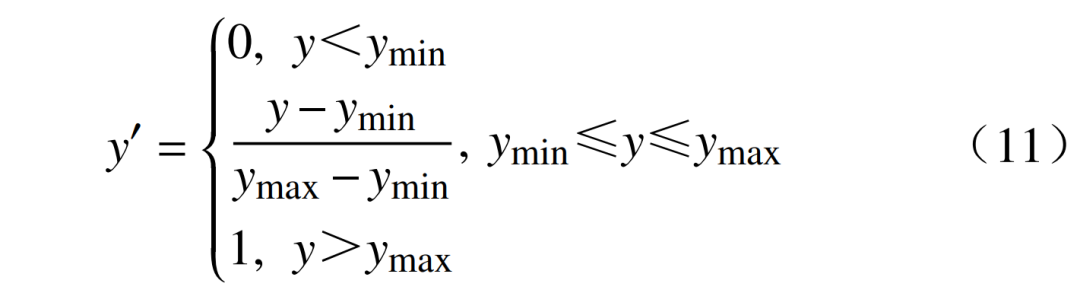
式中：为归一化处理后的数据；y为初始采集测量数据；ymin、ymax分别为数据集的最小值和最大值。

此外，为更好捕捉数据之间的相关性，提高模型对于数据的理解和表征能力，需要提高一维输入数据y=维度，其中d为测量量的数目。提升维度后的二维矩阵为

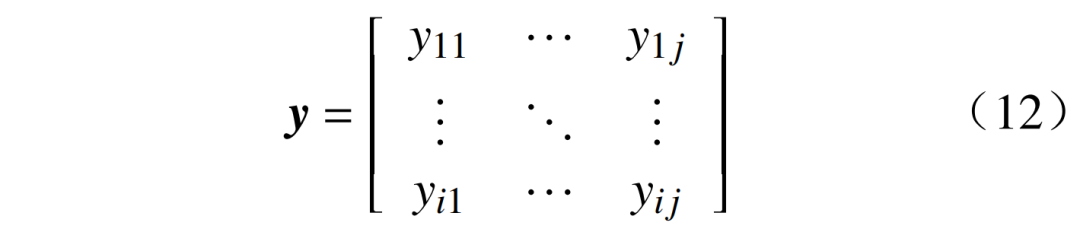
式中：yij为第j个样本第i个变量的值。

提升维度后测量量的数目应保持不变，则须满足d=i×j。

随后，利用构建好的CNN-LSTM结构，读取预处理后的测量数据，并以输出数据和状态变量之间的误差方差作为整个网络的损失函数l，即

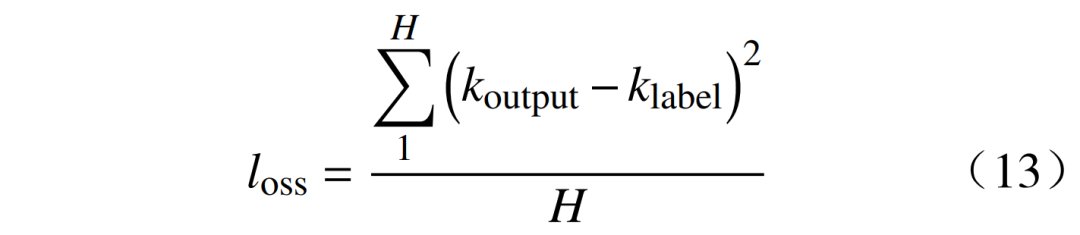
式中：H为状态变量的个数；koutput为CNN-LSTM的预测值；klabel为状态变量的实际值。

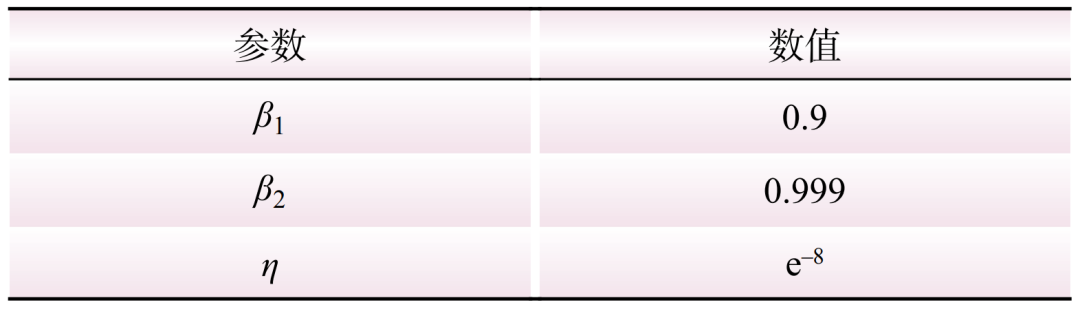
离线训练时，输入层神经元数目为128，LSTM模型神经元数目为128，卷积层和池化层的核尺寸均为。同时，选择Adam算法代替传统随机梯度下降算法，用于调整神经网络训练过程中的权重和偏置参数，通常配置的参数如表1所示。通过在数据迭代过程中对参数进行精细调整，成功将网络的损失函数值降到最小。接着，采用实验性的方法确定最优的迭代轮次和批量尺寸，由此可知最优的迭代轮次和批量尺寸分别为50和64。最后，采用贝叶斯优化算法调整学习率和丢弃率，最优值分别为0.001和0.341。

表1  Adam参数设置

Table 1  Adam parameter settings

CNN-LSTM模型训练完成后，可将配电网实时测量数据，包括节点电压幅值和相角，输入该模型，通过前向计算实现配电网的在线状态估计。在未考虑噪声影响的情况下，各节点的电压幅值和相角估计值与实际值非常接近，显示出良好的状态估计性能，如图6和图7所示。

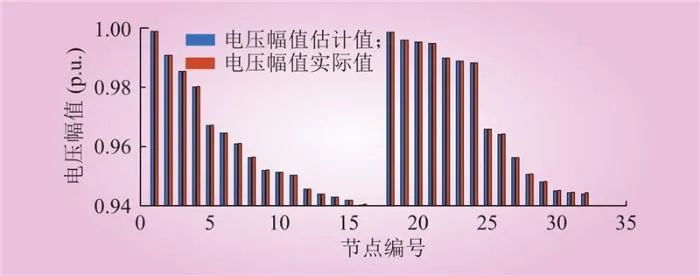
图6  各节点电压幅值状态估计结果

Fig.6  State estimation results of the voltage magnitude at each node

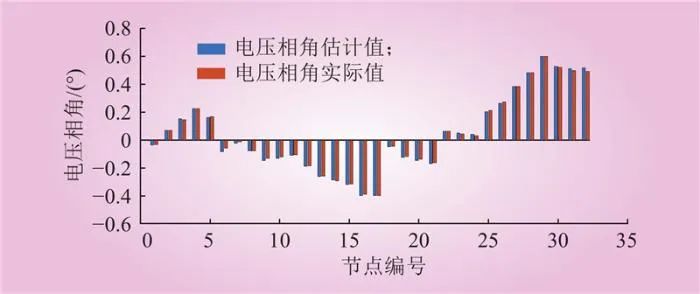
图7  各节点电压相角状态估计结果

Fig.7  State estimation results of the voltage phase angle at each node

然而，由于测量仪器精度限制以及传输中数据丢失，实际测量值会存在一定的误差。因此，本节对所有节点的测量值添加0.5%高斯噪声，并将节点2电压幅值和相角的绝对误差作为结果展示，如图8所示。

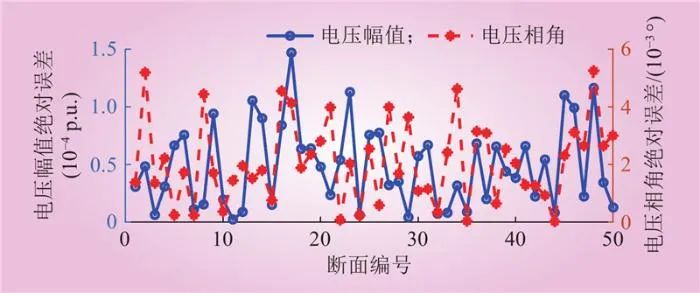
图8  不同断面下节点2电压幅值和相角绝对误差

Fig.8  Absolute error of the voltage magnitude and phase angle at node 2 across different sections

由图8可知，节点2电压幅值和相角的最大绝对误差分别为断面17的1.48×10–4和断面48的5.25×10–3，即使在添加高斯噪声的情况下，所提方法也展现出较高准确性，表明其适用于实际配电网的状态估计。为探究CNN-LSTM组合模型相较于单一CNN模型，以及GAN相较于高斯混合模型（gaussian mixture model，GMM）对状态估计结果的影响，所有节点的测量值均添加1%高斯噪声，并采用平均绝对误差（mean absolute error，MAE）作为衡量标准，即

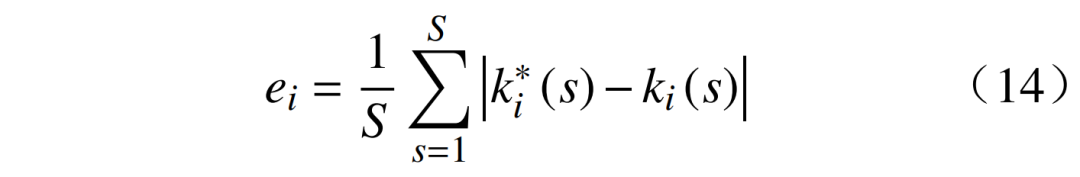
式中：ei为第i个状态量的平均绝对误差；

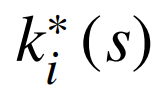
为s断面第i个状态量的估计值；ki(s)为s断面第i个状态量的实际值；S为断面总数。

各节点电压幅值和相角的MAE如图9~10所示。

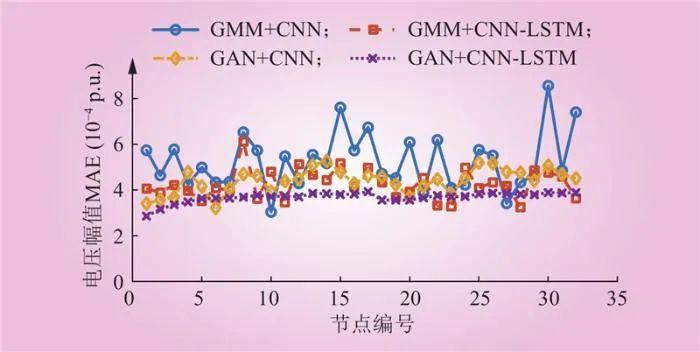
图9  4种预测模型电压幅值MAE的比较分析

Fig.9  Comparative analysis of the MAE for voltage magnitude across four prediction models

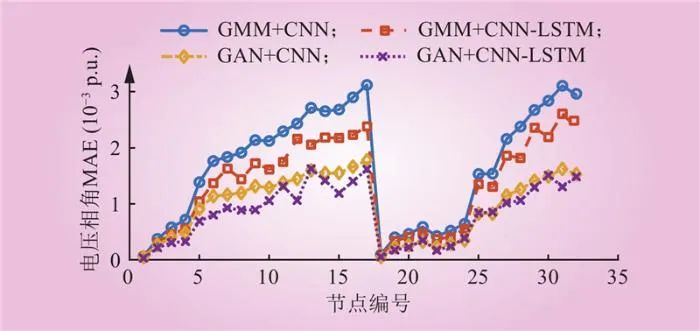
图10  4种预测模型电压相角MAE的比较分析

Fig.10  Comparative analysis of the MAE for voltage phase angle across four prediction models

由图9和图10对比分析可得，GAN+CNN-LSTM模型在电压幅值和相角的MAE上均表现出最佳的状态估计效果。特别是与GMM+CNN和GMM+CNN-LSTM的比较中，可观察到组合模型的优势。虽然GMM+CNN-LSTM改善了单一CNN模型的性能，但GAN+CNN-LSTM在使用GAN生成的数据进行训练时，显示出更高的精度和泛化能力。体现了GAN在生成更符合实际状态数据集方面的优势，从而为状态估计提供了更准确的基础。

最后，选择WLS作为对照算法，并引入伪量测来解决WLS算法可观性不足的问题，以评估所提方法的有效性。考虑2%的测量噪声，2种方法作用下，节点5电压幅值和相角MAE的比较分析如表2所示。

表2  节点5电压幅值和相角MAE的比较分析

Table 2  Comparative analysis of the MAE for voltage magnitude and phase angle at node 5

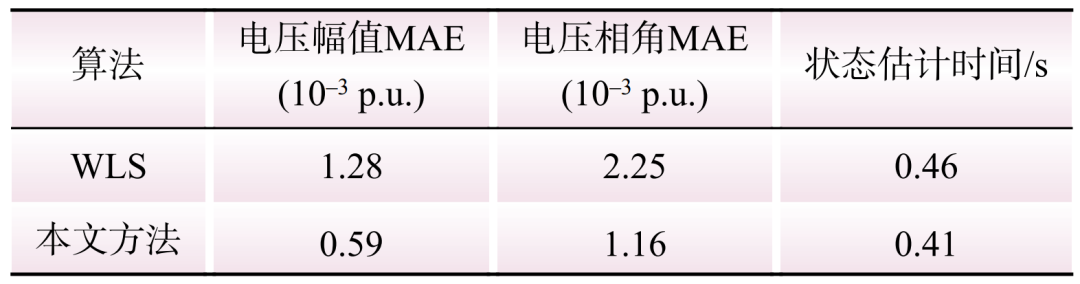
由表2可知，在噪声影响下，所提方法比WLS具有更高的精度，电压幅值和相角的MAE分别降低了约53.91%和48.45%。在计算效率方面，所提方法状态估计的实时性明显优于WLS方法，效率提高了10.86%。

4.2  IEEE 123节点算例分析

为验证所提状态估计算法在较大规模网络上的有效性，本文选择IEEE 123节点配电网作为研究对象，其拓扑结构和实时量测装置位置如图11所示。数据集的构建方式与IEEE 33节点网络的案例研究相同。离线训练CNN-LSTM模型时输入层的神经元数量为488，卷积核和池化核的大小均为，LSTM神经元数量为256，采用最大池化策略。最优学习率和丢弃率分别为0.001和0.334，训练轮次为80，批量尺寸为256。在不考虑噪声影响的情况下，各节点电压幅值和相角的MAE如图12所示，MAE控制在5×10–3以内，展现出较高的准确性。

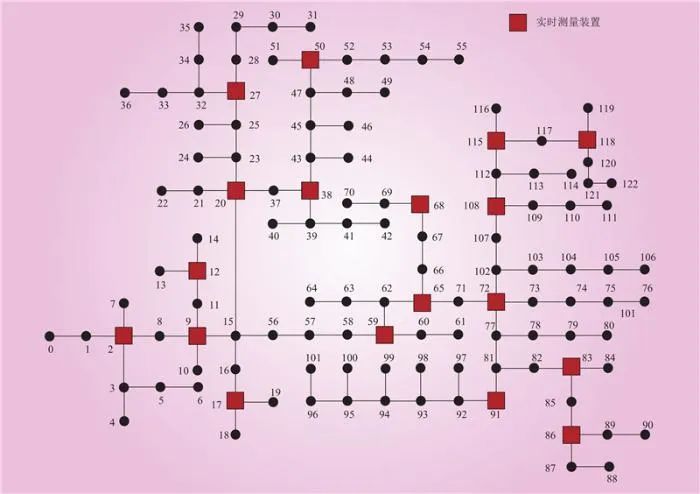
图11  IEEE 123节点配电网测量配置

Fig.11  Measurement configuration of the IEEE 123-node distribution network

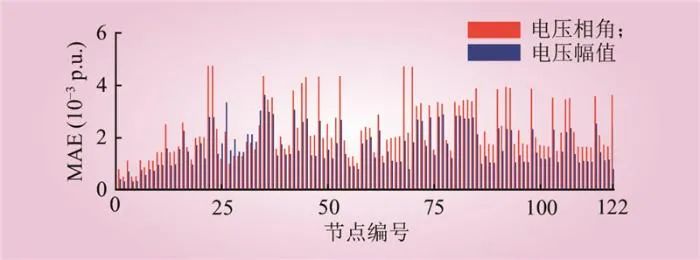
图12  各节点电压幅值和相角的MAE

Fig.12  The MAE of the voltage magnitude and phase angle at each node

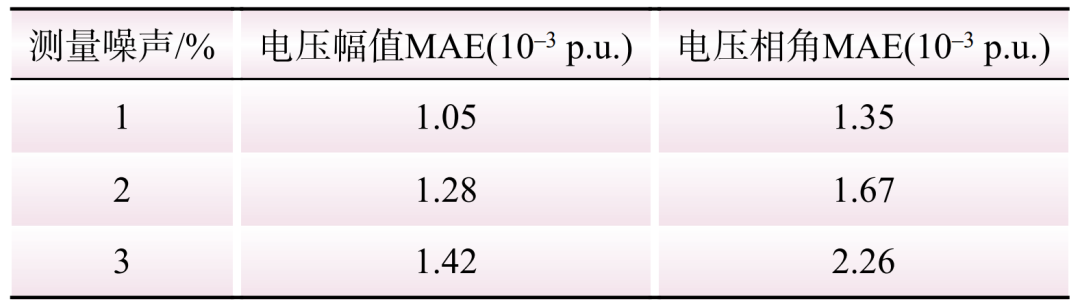
为分析噪声对估计准确性的影响，本节设计了3种不同的测量误差：1%，2%和3%，不同量测误差条件下，电压幅值和相角MAE的对比结果如表3所示。结果表明，虽然测量噪声的提高使预测精度略有减少，但总体来看MAE仍维持在一个相近的误差范围内，显示了所提方法对于测量噪声具有良好的鲁棒性。这一结果对于配电网的状态估计尤其重要，证明了即使在不完全的量测条件下，该方法也能提供可靠的数据分析。

表3  不同测量噪声下节点9电压幅值和相角的MAE

Table 3  The MAE of the voltage magnitude and phase angle at node 9 with different measurement noise

05

结论

针对实时测量数据缺乏时配电网状态估计精度受限的问题，本文提出了一种基于贝叶斯优化CNN-LSTM的配电网状态估计方法，得到以下主要结论。

1）贝叶斯优化算法在调整CNN-LSTM超参数时能够显著提高寻优效率，节省时间资源，同时增强模型性能。

2）利用IEEE 33节点和IEEE 123节点配电网进行仿真，结果表明，即使在较大高斯噪声影响下，估计精度依然保持在较高水平，MAE维持在较小范围内，显示了良好的鲁棒性和稳定性。

3）与传统WLS相比，所提方法在噪声环境中的电压幅值和相角估计精度分别提高了53.91%和48.45%。此外，本方法在计算效率上也有显著提升，为提高配电网的运行效率和供电可靠性提供了强有力的技术支持，具备重要的实践意义。