考虑虚拟电厂的电力系统一致性经济调度方法

考虑虚拟电厂的电力系统一致性经济调度方法

摘要

分布式算法在解决大规模系统的控制问题方面显示出巨大的潜力。将领导者-跟随者增量成本一致性算法（lead-follower incremental cost consensus algorithms，ICC）扩展为无领导者的分布式调度优化算法。所提出的无领导增量成本一致性（leadless incremental cost consensus algorithms，LICC）算法能够连续跟踪系统的负荷差，并在没有领导者的情况下调度发电机。此外，建立了虚拟电厂的分布式经济调度模型，并将其与一致性算法相结合。在Matlab/Simulink和RT-LAB中搭建了一个基于IEEE 14节点系统的动态模型，以验证算法的可行性。该系统包含发电机与虚拟电厂，并配有频率控制和电压调节功能。在实时电力系统仿真模拟器上演示了LICC算法的有效性。

01问题描述

本文采用信息-物理结构对电力系统进行分布式控制调度，其结构示意图如图1所示。图论适用于分布式控制算法的设计。可以选择发电机或负载的连接点作为分布式代理。在经济调度过程中，发电机是需要考虑的主要因素。每台发电机（或总线）都可视为图中的一个节点。假设有一个环形拓扑结构的5节点通信网络，该网络可以用相邻矩阵来表示。

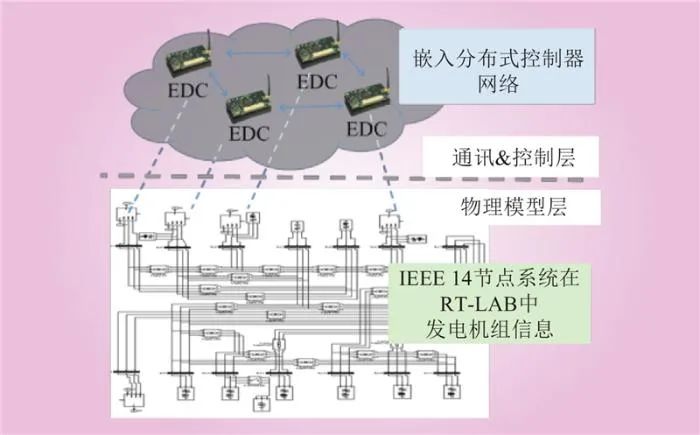
图1  分布式控制信息-物理电力系统

Fig.1  Distribute Controlled Cyber-Physical Power System

经济调度问题的数学模型通常可以表示为一个优化问题，其中目标函数是总发电成本，约束条件包括功率平衡、机组出力限制等。

每一个发电机的发电成本可用二次型表示为

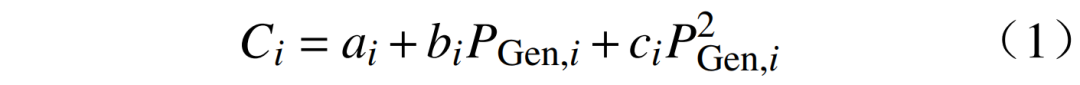
式中：Ci为发电机（发电厂）i的发电成本；P,i为发电机i的发电量；ai、bi、ci分别为相应的发电成本参数。

经济调度问题的目标函数为系统内所有发电厂和机组的发电成本最小，即

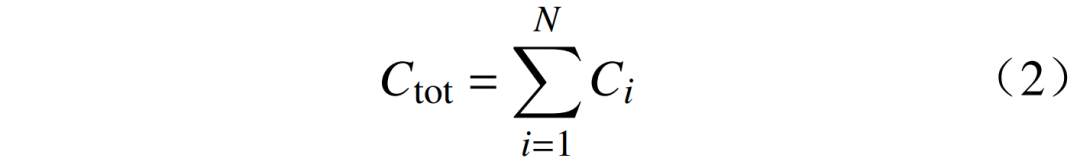
式中：C为所有N个发电厂的总发电成本之和。

传统经济调度问题的约束条件主要为源-荷功率平衡以及机组出力功率限制。

对于虚拟电厂而言，其是聚合多种类型可调资源的电力市场参与主体，经济调度模型以虚拟电厂最小运行成本F为目标。本文中，可调度资源包括各分布式能源和微型燃气轮机的发电成本，以及储能装置的充放电成本，即

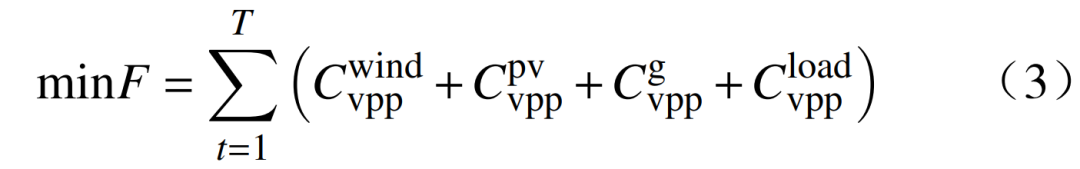
式中：

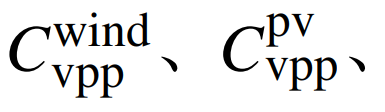
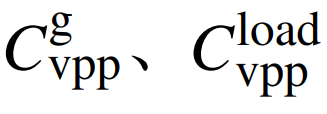
分别为虚拟电厂中的风机发电成本、光伏发电成本、燃气轮机发电成本和可控负荷的运行成本；T为总时间。

风机和光伏的发电成本为零，因此虚拟电厂的出力成本由可控负荷成本与小型燃气轮机的发电成本组成，即

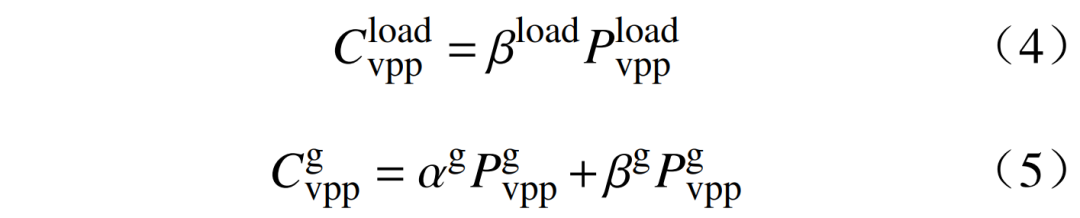
式中：为可控负荷的成本系数；、分别为小型燃气轮机的成本系数；

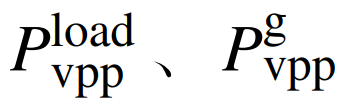
分别为可控负荷功率、燃气轮机功率。

约束条件如下。

1） 虚拟电厂的上送功率为

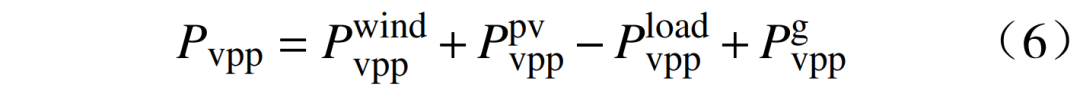
式中：P为虚拟电厂向电网上送的功率净值总和；

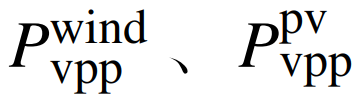
分别为虚拟电厂的风机、光伏功率。

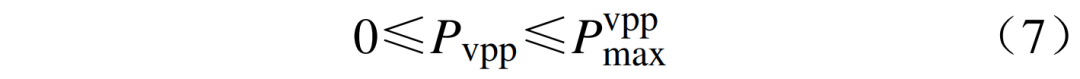
式中：

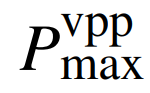
为虚拟电厂向电网输送功率上限。

2） 微型燃气轮机约束为

式中：

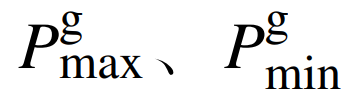
为微型燃气轮机的出力上、下限。

3） 可中断负荷约束为

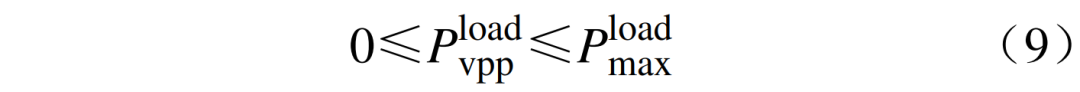
式中：

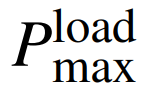
为虚拟电厂区域的最大负荷。

虚拟电厂的出力成本与传统发电厂相似，可以用凸函数的方式进行表示。

02

含增量成本的无领导者一致性算法

传统的优化方法求解EDP受制于计算资源，难以在大规模电力系统中落地应用。提出一种考虑增量成本的无领导者一致性算法以分布式地求解EDP。

定义yi(k)为第k次迭代时第i个节点的局部功率失配，即

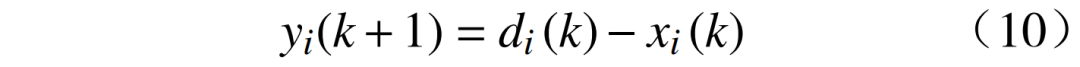
式中：di(k)为第k次迭代时第i个节点的实际功率需求；xi(k)为当前节点的潮流流入功率。

由于每台发电机的增量成本在最优点都是唯一的，所以当系统达到最优运行点时，应满足以下条件：1）总功率是平衡的；2）在不违反约束的情况下，各发电机组的增量成本在最优值上达成一致。

为了以分布式方式解决这一问题，首要目标是估算总功率失配。将yi定义为第i个节点上总失配的分布式估计值。结合文献，LICC的更新规则为

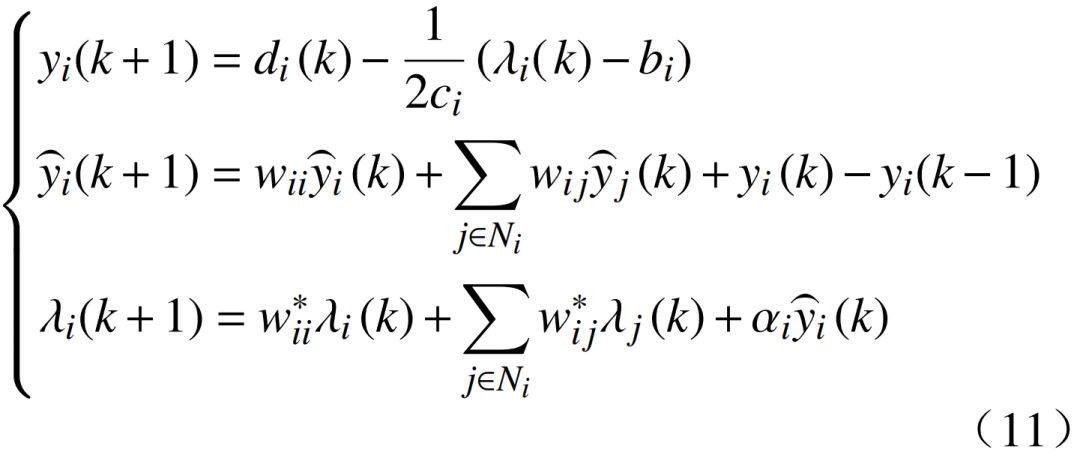
式中：αi、bi、li均为机组发电成本参数；

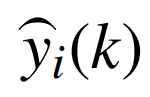
为第k次迭代时第i个节点上总失配的分布式估计值；wij为加权更新矩阵中i行j列的元素；

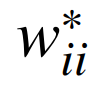
为一致更新矩阵中i行j列的元素；λj(k)为第k次迭代第i个节点的功率参数值；di为第i个节点相应参数。

第i个节点的功率需求di(k)对系统来说是未知的，可以看作是系统的局部输入。这是一种分布式算法，因为每个控制器只需要其一阶邻居和自身的信息，不需要多阶路由算法。分布式算法可以看作一个离散时间线性系统。由于只使用了真实的局部功率失配信息作为反馈，因此会自动处理生成限制。

03考虑发电机动态特性的模拟试验台

为了在现实场景中验证所提出的LICC，考虑了一个修改的IEEE 14节点测试系统作为模拟测试平台。其中，3台发电机和两个虚拟电厂提供总负荷，1-3号为传统机组，4-5号为虚拟电厂定义的每台发电机的燃料成本函数，目标是在保证电能质量的同时解决EDP问题。分布式可控电力系统由3层系统组成，即控制层、电网层和通信层。通信层模拟的是复合网络的行为，如时间延迟、数据包丢失或链路故障。控制层由分布式控制智能体组成。在电力系统层，每台发电机都配备了自动发电控制和自动电压调节器。每次迭代，控制层的计算结果都会发送给电网层中相应的发电机。本节将讨论电网模型和详细的发电机模型，并演示算法的控制层。所有仿真均在Matlab/Simulink以及实时电力系统仿真器RT-Lab上进行。为了使发电机预先执行经济调度并维持电能质量。采用自动发电控制进行频率调节。出于同样的原因，自动电压调节器也包含在发电机系统中。频率和电压被分开控制，频率由原动机系统控制，电压由励磁系统调节，相应系统如图2所示。

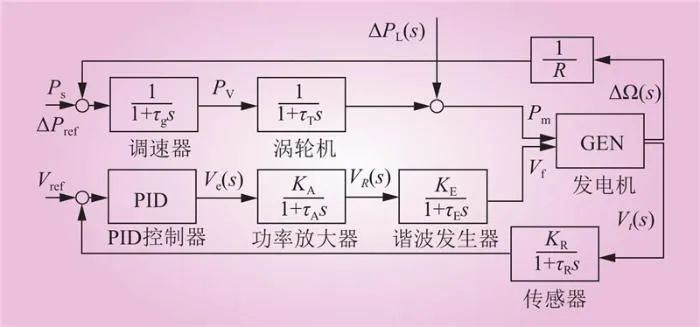
图2  发电系统示意

Fig.2  Generation System Illustration

本文发电机的参数为：额定输出功率Pn=200 MW，额定相电压Vn=15 kV，频率fn=60 HZ，极数=20，发电机惯性常数H=2.9。选择IEEE 14节点测试系统作为LICC算法的测试平台。输电线路模型采用型等效电路；用5阶系统表示发电厂动态特性，验证一致性算法在具有动态特性系统中的可行性。控制层的拓扑结构为全连接。在无领导算法中有两个层次的一致性。第一层是对总功率失配的估计。第二层是对发电机的增量成本一致性变量。第二层相关细节可以从文献中查询。所提出的三层系统已在Matlab/Simulink以及商用实时电力系统模拟器RT-LAB中实现。

因为考虑了动态特性，基于Simulink的仿真验证将较为耗时。为了满足验证一致性算法在考虑电力系统动态特性时的效果的需要，采用RT-LAB平台对电力系统模型进行实时化建模与仿真。RT-lab用状态空间节点法（state space nodal method，SSN）将模型分解为多个相差单步长的子系统，在下位机中实现高速并行计算，从而达到实时仿真的目的。本文采用的主机处理器为Intel i5处理器，8核16线程架构，下位机设备型号为OP4510，包含12个并行处理器核心。

04仿真结果

采用基于IEEE 14节点测试系统。初始化后，将在第s时向系统添加100 MW的额外负荷，用于测试LICC控制系统的响应。系统有5台发电机，N=5；总负载由所有发电机分担。

在求解电力系统EDP时，增量成本是关键特征，也是所提出LICC算法的第二层一致性。第一层一致性、相电压和系统频率也是验证算法的重要因素。LICC实施后系统的稳定性和电能质量得到了有效证明。在一致性算法调整各发电单元出力的过程中，整个电力系统的频率仍然保持在国家标准之内，各节点电压也在0.95~1.05的范围内。在考虑电力系统动态特性的情况下全系统的电能质量仍然满足调度要求。此外，在LICC算法中，设计了2个参数控制增量成本收敛速度。

本文给出了考虑电力系统动态特性的Matlab-Simulink模型的仿真结果。如果收敛迭代次数大于100次，将结果设为100。通过研究可以初步推测出正标量μ和收敛系数α的最佳参数。不同控制参数设置下收敛时间的比较如图3所示。图3 a)为不同参数下的收敛迭代。由于涉及电力系统动态特性，因此这种模拟比实时更慢。在英特尔酷睿i5台式电脑上，一个实验，100次迭代需要5个小时。图3 b)显示了不同参数下的收敛时间。实时仿真结果趋势与计算迭代吻合。因为RT-lab时实时仿真，因此可以快速优化整个系统的控制参数，帮助算法提升收敛速度。

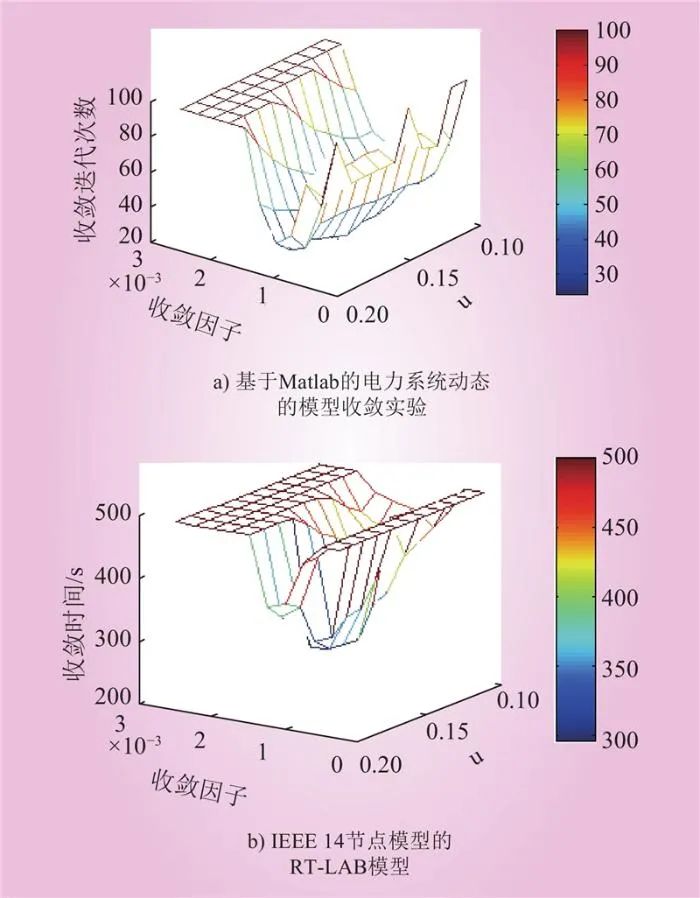
图3  不同控制参数设置下收敛时间的比较

Fig.3  Comparison of convergence time with different control parameter settings

在所提出的LICC算法中，对通信网络层做出了修改，人为增加通信噪音。本文所提算法中，各控制器之间所交互的信息为

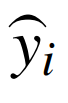
和yi，即第一层与第二层的功率失配值。因此，将失配值添加5%大小的噪声，并通过通信网络，向其他的控制器发送带噪声的失配值。整个系统中负荷的变化没有噪声产生，所以各个节点所检测到的功率失配理论上也应没有波动。但是由于通信网络中的噪声，第一层功率失配值和第二层功率失配值都会产生噪声。从增量成本的角度来说，噪声条件下仍然可以满足经济调度优化的收敛需求。

可扩展性是分布式算法最重要的特征之一。当正标量µ=1/10，收敛参数α=0.001时的仿真结果如图4所示。

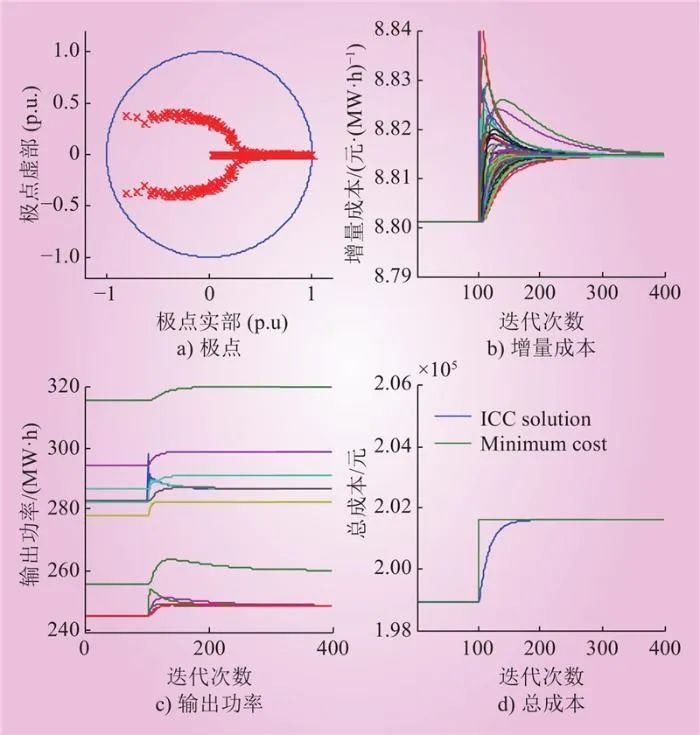
图4  当µ=1/10, α=0.001时的仿真结果

Fig.4  The simulation result when µ=1/10, α=0.001

图4显示了100个电机的增量成本能够在400次迭代中就新的操作点达成一致性。靠近需求增加节点的发电机首先提高其输出功率的设定点，然后，其余的发电机逐渐提高其输出功率的设定点，以分担负荷。出现这种行为的原因是，当网络变大时，信息的传播需要更多的迭代。综上可知，所提出的LICC算法具有很高的可扩展性。

05结语

针对集中式电力系统经济调度算法难以有效处理海量的数据流，本文在ICC算法的基础上提出了无领导者的LICC算法，求解含有虚拟电厂的电力系统经济调度问题。由于一致性算法的效果受限于通信层拓扑连接方式，而随着极端气候与自然灾害的增加，拓扑变化对新型电力系统调度的影响不可忽视。在本文的基础上，未来研究方向包括进一步分析不同通信拓扑下的最优加权参数设计，以及提高LICC算法在不完善通信网络拓扑下的韧性。