计及电力市场交易机制的风-光-储-氢混合电厂配置策略研究

摘 要 新能源发电正经历从保护性并网模式迈向电力市场竞争模式的转型。然而，由于新能源发电的不确定性和间歇性，难以独立有效地参与电力市场竞争。为此，本文构建了一种基于新能源场站的风-光-储-氢混合电厂模型，旨在稳定供应电力、参与电力市场交易和满足氢能负荷需求。在电力市场环境下，以资产收益率(return on equity，ROE)最大化为原则，结合中长期与现货市场交易规则，建立双层优化配置模型；外层采用改进的麻雀搜索算法(improved sparrow search algorithm，ISSA)寻求最优配置策略，计算ROE作为适应度数值，内层采用混合整数线性规划求解具体运行策略。同时，引入电解槽产生氢气的二次多项式约束，并将其松弛转化为混合整数二阶锥规划(mixed-integer second-order cone programming，MISOCP)问题，形成混合电厂的优化配置方案。案例仿真结果显示，优化配置方案的ROE可达0.32，通过制氢效率特性的进一步优化运行，ROE可提升至0.35，实现了电能与氢能的有效融合，显著增强了新能源发电在电力市场中的竞争力。

关键词 电力市场；新能源发电；氢储能；电化学储能

随着全球能源转型的加速推进，电力市场逐步成为能源优化配置的主要平台。电力市场通常分为中长期交易和现货交易。在中长期交易中，新能源发电的间歇性和不确定性，使其难以满足高精度交易需求，增加了偏差考核成本。而在现货市场中，新能源发电波动性加剧了市场供需复杂性，且其低边际成本将导致市场价格下行，不利于市场稳定发展。然而，储能和氢能技术与新能源的融合发展显著增强了新能源参与市场化交易的竞争力，由此形成的风-光-储-氢混合电厂成为人们关注的热点。

针对混合电厂的配置策略，谢金勇等和赵晶晶等研究碱性电解槽和质子交换膜电解槽协同优化配置方法，基于随机优化生成典型场景，分别采用混合整数线性规划和非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA-Ⅲ)进行求解；徐衍会等针对离网制氢系统，计及碳排放因素，构建多目标优化系统，采用改进NSGA-Ⅲ-GT求解；张彦虎等在电-氢储能的基础上，提出了一种风-储-氢-氨优化配置策略，并针对四种工作情景，进行详细的经济性分析；向昱瑾等构建双层配置策略模型，上层进行容量配置，下层计及运行策略，采用麻雀搜索法算法(SSA)配合混合整数线性规划进行求解；谭玲玲等计及碳交易机制，构建双层配置策略模型。伊国通等考虑风电、光伏出力的不确定性，构建基于数据驱动的两阶段分布式鲁棒优化配置策略，考虑最恶劣场景后，获得比上述随机优化更好的经济性。但上述方法，均基于历史数据构建典型场景，作为配置策略的研究对象，储能载荷状态的平衡约束被局限于短周期分析，无法充分展现储能系统在跨周、跨季度等长周期调节中的优势。丁琦欣等提出了一种基于年度数据的电氢微网凸松弛规划模型，有效缩减原问题计算时间。Wu等基于全景时序数据模拟，根据电化学储能和氢储能的不同调节能力，设置三级储能系统，构建多时间尺度两阶段混合储能配置模型。虽然采用了全景时序数据模拟，但其构建的规划模型无法与电力市场中的日前-日内偏差考核机制相互结合，基于电力市场为边界条件的配置策略模型尚未建立。

本文针对新能源发电独立参与电力市场化交易的问题，构建风-光-储-氢混合电厂，并探索其市场化交易策略。首先，提出基于电力市场化交易规则的双层优化配置模型，外层采用ISSA寻求最优配置策略，计算ROE作为适应度数值，内层建立规划计及运行的双层结构模型，并将规划决策变量作为运行优化中相关决策变量的约束条件直接嵌入，实现规划与运行的一体化求解；其次，优化产氢效率，引入电解槽产生氢气的二次多项式约束，并将其松弛转化为混合整数二阶锥规划(MISOCP)问题。最后，通过案例仿真分析，探讨电化学储能、氢储能在混合电厂中的作用，研究中长期合约机制对混合电厂配置策略的影响，验证所提模型与方法的有效性。

1 混合电厂参与电力市场交易

1.1 混合电厂构成

本文研究的混合电厂的构成如图1所示，包括风电场、光伏电站、电化学储能系统以及氢储能系统(具体涵盖电解槽阵列、氢压缩机与氢储罐等关键设备)。

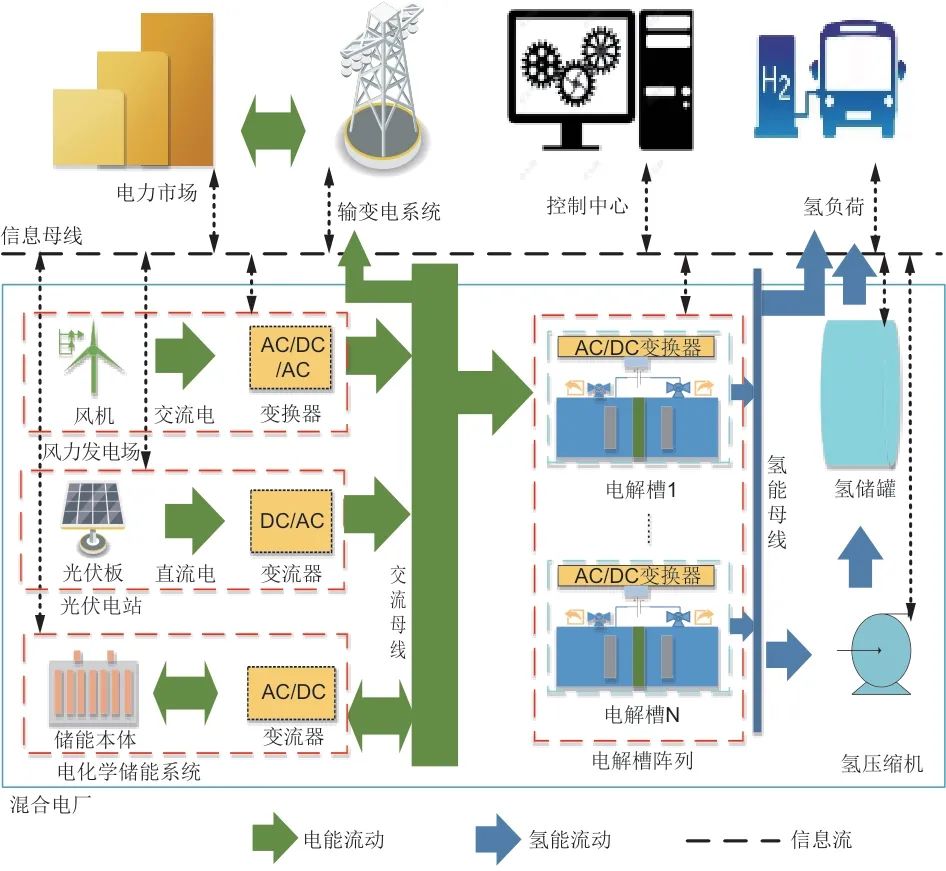
图1   混合电厂构成图

1.2 电解槽的效率特性

本文选择技术成熟且应用广泛的碱性电解槽(alkaline water electrolyzer，AWE)作为研究对象。根据研究内容，绘制了10 MW电解槽的产氢量和效率曲线，如图2所示。为了方便后续求解使用，本文利用最小二乘法对图2中绿颜色曲线的输入功率与产氢量相关数据进行了拟合，得到式(1)

其中，A=-0.0774，B=21.5757，C=-11.7851。

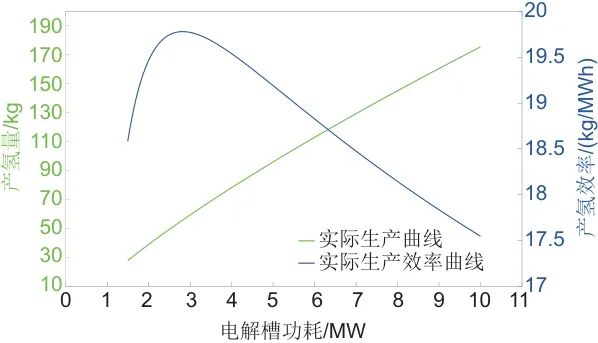
图2   典型电解槽产氢量及效率曲线

1.3 中长期交易结算方式

1.3.1 中长期合约分解

随着中国电力市场建设进程的不断推进，初步形成了中长期合约规划供需，现货市场调整偏差，共同维持市场平衡的格局。电力市场交易体系通过小时级电量分解曲线，实现中长期交易与现货交易的有效衔接，常用的3种方法为峰谷平曲线法、全天平均曲线法及高峰时段曲线法，如图3所示。在本文后续研究中，将提供年度电力总负荷需求，作为新能源电站需在中长期内交付的电量约束。具体做法是，将年度负荷总量等比例划分至每日，得到每日的交易电量；随后结合图3所示的典型负荷曲线进行时序分解，构造典型日负荷曲线。电量分解曲线方法不仅使得中长期合约电量在日前市场中得以体现，也为实时市场中的物理交割奠定基础，实现中长期与实时交易的协同对接。

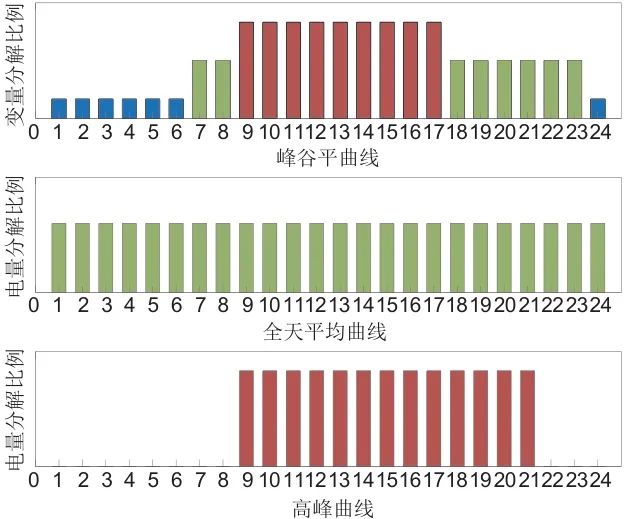
图3   合约分解曲线

1.3.2 中长期合约与现货市场的衔接

发电侧电量结算包括中长期合约、日前市场和实时市场结算。本文采用式(2)~式(4)完成日清算，日前中标电量按日前节点价格结算，中长期合约按合约价与日前价差结算，偏差电量按实时市场价格结算。在此框架下，电力负荷与混合电厂通过中长期交易建立金融合约，混合电厂同时参与现货市场获取即时收益。

2 混合电厂经济效益测算模型

2.1 目标函数

本文选取ROE为经济效益的主要评价指标，从投资和收益的角度出发，寻求最佳的系统配置方案。目标函数如式(5)所示

2.1.1 经济收益

2.1.2 资产投入

资产投入部分分为工程建设投资和运行维护成本。具体的分项工程名称如表1所示，系统配置优化的决策变量为~。

表1   分项工程与变量

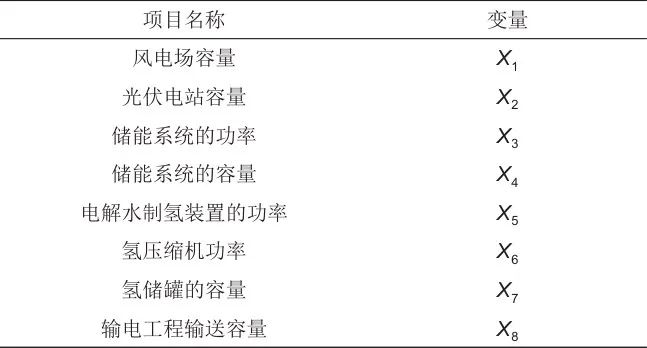
（1）工程投资成本

2.2 约束条件

2.2.1 储能系统运行约束

储能系统的充放电功率约束以及储能本体容量约束如式(15)~式(19)所示

2.2.2 氢储能运行约束

2.3 基本配置策略与算法流程

2.3.1 基本配置策略

本文构建优化投资策略，以匹配电力负荷与氢能需求，最大化新能源项目投资效益。

（1）现货市场交易电量：混合电厂参与电力现货市场的电量不超过新能源年发电量的20%。

（2）电化学储能定位：优先储存新能源电力，剩余容量用于现货市场套利，以确保新能源供电的稳定性。

（3）电解水制氢策略：电解水制氢系统所需电能完全来自新能源，避免从电网购电，确保氢气为“绿氢”。

（4）输电线路配置：外送能力上限设定为中长期负荷每小时平均用电功率的3倍，以适应电网接纳能力。

（5）系统工作时间：全年工作7320 h，设4次15天检修期，由火电厂承接中长期负荷，确保供电稳定。

2.3.2 双层规划算法

本文以最大化ROE为优化目标，所构建模型具有多重复杂特性，难以直接采用商业求解器求解。首先，目标函数中包含变量之间的除法项，构成非线性结构；其次，式(1)中的约束为非凸的二次等式约束，松弛转换后，系统模型为混合整数二阶锥规划(MISOCP)问题；此外，模型中还广泛存在0~1变量与连续变量的乘积项，进一步加剧了模型的非线性。这些因素综合在一起，导致模型的求解成为复杂的混合整数非线性规划(MINLP)问题，现有主流商业求解器很难同时处理上述三种情况构成的模型，群智能优化算法在处理此类问题时也面临收敛速度慢、全局性差等挑战。

为提升模型可解性与计算效率，本文设计了一种分层优化策略。通过构建双层优化模型，将容量配置与运行调度相对分离。外层为规划层，采用改进麻雀搜索算法(ISSA)在可行域内搜索最优容量配置；内层为运行层，在给定容量配置的前提下，调用GUROBI求解器对运行策略进行精确优化。在建模实现方面，本文基于MATLAB环境，采用YALMIP工具箱构建模型框架，统一描述目标函数、决策变量和约束条件。YALMIP可以自动处理0~1变量与连续变量的乘积项，通过big-M方法对其进行线性化，转化为标准MILP约束形式；同时，YALMIP还支持动态变量边界传递，有效支撑双层结构中变量间的联动约束。而且GUROBI可以直接求解MISOCP问题，特别适用于大规模混合整数规划问题的求解。通过上述分层求解框架和求解工具的使用，可以实现对非凸、非线性复杂优化问题的求解，同时保持模型结构表达的灵活性与决策结果计算的高效性。

如图4所示，本文基于ISSA与GUROBI实现对双层规划-优化问题的求解，以实现系统容量配置与运行调度的一体优化，其中ISSA算法参考了李圣清等，具体流程如下。

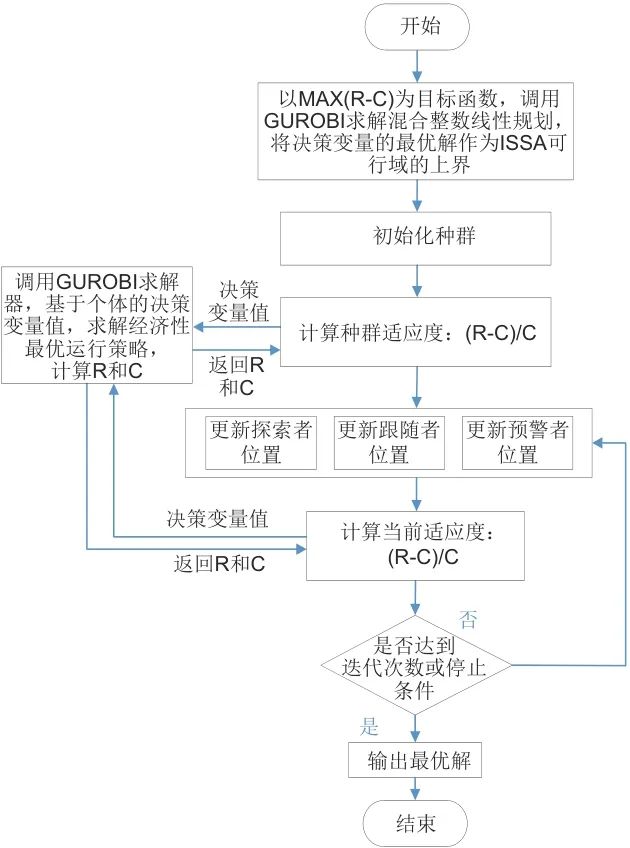
图4   优化流程图

（1）可行域计算：以最大化收入(R-C)为目标，基于YALMIP动态变量边界传递，结合松弛方法将非凸的二次等式约束转化成二阶锥约束；再调用GUROBI求解器，求解出规划变量(系统容量配置)的可行解，作为ISSA的初始可行域上界，精确搜索空间；

（2）初始化：首先利用Circle混沌映射初始化种群，在可行域内配置规划变量，生成多个随机解，形成种群个体初始位置信息；

（3）内层运行优化：对于种群中每一个个体(即一组容量配置解)，调用YALMIP建模+GUROBI求解器，对运行阶段的调度问题进行精确求解，得到对应的系统成本与收益，后续反馈给外层算法，用于计算ROE，作为该个体的适应度值；

（4）位置更新与扰动机制：在ISSA算法中，通过引入黄金正弦公式改进探索者位置；引入动态权重因子和莱维飞行策略使得跟随者可以更好地探索全局空间；在种群中随机选取10%~20%麻雀作为预警者；同时，在迭代的前期、中期、后期，当全部麻雀完成位置更新后，分别利用柯西分布、t分布和高斯分布函数选择最优个体进行扰动更新，并结合贪心策略对更新解进行筛选过滤，保留混合变异扰动后的更优位置，以提升最优解的质量；

（5）迭代与收敛：重复执行适应度评估与位置更新，直到满足最大迭代次数或收敛准则，输出ROE最优解及对应的容量配置方案与运行策略。

3 典型场景构建与配置方案分析

3.1 典型场景构建

本文基于日前市场衔接中长期交易和实时市场计算售电收益。中长期电量通过负荷曲线分解，电价取历史合约均值；新能源实时出力和现货市场电价采用真实数据，而日前出力与电价需构建预测数据集。为此，本文采用预测值校正框架，将预测误差视为随机变量(数据噪声)，即实际值与预测值之差，见式(32)。

3.1.1 新能源数据

新能源实时数据：新能源出力曲线如附图B1、B3所示。新能源误差概率密度如附图B2、B4所示。

3.1.2 电价数据

电力现货市场实时价格曲线如附图B5所示，日前市场误差概率密度如附图B6所示。

3.1.3 负荷数据

负荷需求如表2所示。

表2   负荷需求

为模拟氢能负荷需求，首先根据表2所示的年度总需求量计算出日均需求水平；随后参考Lu等提出的多种氢能负荷类型曲线，选取波动较小、负荷相对稳定的工业(化工)用氢典型负荷曲线作为代表。在此基础上，按照每日氢气需求总量对所选曲线进行归一化缩放，生成典型日的分时需求曲线，如附图B7所示。

3.1.4 其他边界条件

具体计算中涉及到的参数，详见附录C1、C2、C3。

3.2 配置方案分析

3.2.1 系统配置方案分析

本文针对表2中不同的负荷需求，构建了5种系统配置方案，计算得到的最优容量配置如表3所示。

表3   系统配置方案

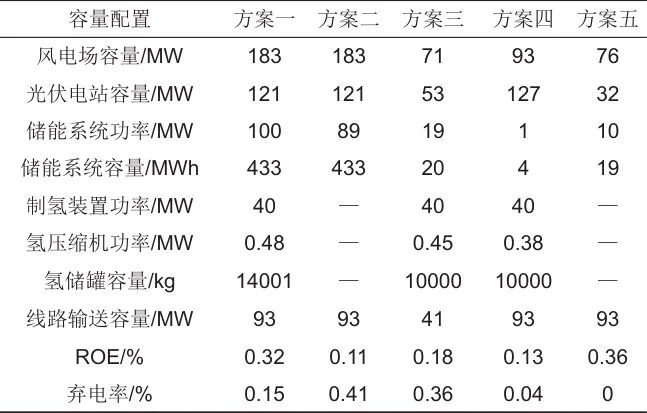
方案一(风-光-储-氢，电力市场交易)：同时满足电力与氢能负荷，中长期负荷按峰谷平曲线分解，参与现货市场交易；

方案二(风-光-储，电力市场交易)：满足电力负荷，中长期负荷按峰谷平曲线分解，参与现货市场交易；\

方案三(风-光-储-氢，不参与电力交易)：仅满足氢能负荷，构建绿氢制备系统；

方案四(风-光-储-氢，传统电力交易)：同时满足电力与氢能负荷，中长期合约不带曲线分解，全年交易额满足中长期电量需求；

方案五(风-光-储，传统电力交易)：满足电力负荷，中长期合约不带曲线分解，全年交易额满足中长期电量需求。

方案三作为不参与电能量交易的绿氢生产系统，在氢气价格为20元/千克时，ROE为0.18，具有一定的经济吸引力。而在传统非电力市场环境中，方案五是一种理想交易模式，适用于新能源发展初期，由于新能源建设成本高，全额优先消纳得以实现。若按最新的风电、光伏及储能系统成本计算，方案五的ROE可达0.36。然而，随着新能源渗透率提高，这种模式已不具备可行性。若在方案五基础上增加氢气生产，形成方案四，由于电价差消失，系统缺乏耦合互补空间，ROE下降至0.13。因此，在非电力市场环境中，方案四并非最佳选择。

在电力市场环境下，方案二具备经济可行性，但ROE较传统模式下的方案五明显降低。方案二依靠储能优化部署减少新能源波动性，确保电力供应稳定，满足中长期电力负荷分解曲线需求。然而，储能的增加提升了成本，尽管峰谷价差提供套利空间，ROE仍然偏低。相比之下，方案一充分利用系统间互补效应与能量转换优势，展现出显著优势。从表3分析可见，氢能系统的引入显著提升整体收益水平，ROE达到0.32，仅次于方案五，远超其他方案。与方案二和方案三相比，方案一不仅具备良好经济效益，还能同时满足电力与氢能负荷需求。

3.2.2 弃电分析

在电力市场环境中，方案二和方案三的弃电率较高，分别达41%和36%，主要因风光发电不连续性所致。若增加储能配置，成本上升将导致ROE显著下降。因此，在风光度电成本较低时，系统通常选择超配新能源，以增强供电稳定性并减少对储能依赖。电解水制氢作为可调负荷，为风光储系统带来优化空间。方案一相比方案二，新能源投资规模未增加，将弃电率降至约15%且改善系统盈利能力。

3.2.3 运行情况分析

本文设定了两种电解水制氢装置的运行策略。

策略一：电解槽产氢效率固定，不考虑多电解槽协同调度，即容量为1台40 MW。

策略二：计及电解槽效率变化，并实施多电解槽协同调度，即容量为4台10 MW。

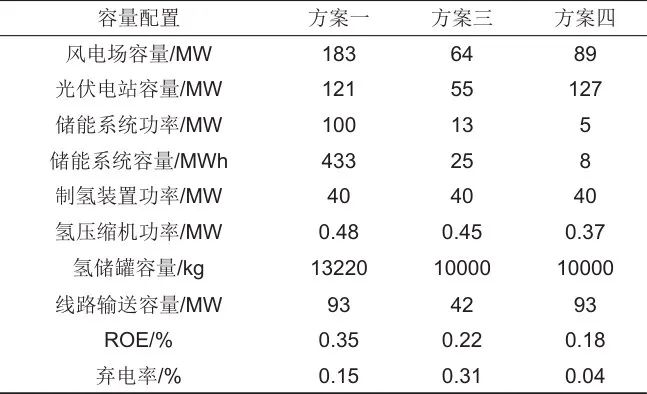
3.2.1节中，使用了策略一，本节使用策略二，配置结果如表4。通过对比表3和表4的配置方案，发现方案一、方案三和方案四的ROE均有所提升，分别提高了3%、4%和5%。方案三与方案四的ROE提升源于效率曲线的使用，增加了氢气产量并减少了新能源投资。而方案一的ROE提升则是因为策略二能根据产氢效率和实时电力价格调整运行策略，从而在保证稳定运行的同时最大化经济效益。

表4   系统配置方案

（1）电化学储能在系统中的作用

策略一和策略二的典型周调度与交易策略分别如附图D1和D2所示，对应的电力价格见附图D3。储能系统在新能源发电高峰时存储多余电能，在发电不足时释放能量，从而有效降低弃电率并提升经济效益。典型周前两天(1~48时段)，新能源出力充足，可满足中长期负荷需求，剩余电量根据储能的荷电状态和氢储罐状态进行分配，储能系统进行充电，电解水制氢装置功率提升消耗过剩电力，此时弃电发生。在第3天至第7天(49~168时段)，新能源出力不足，储能系统介入，维持能量平衡。同时，在电价超过490元/MWh时，储能系统参与现货市场以获取更高经济回报。

（2）氢能在系统中的作用

由于氢储罐对氢负荷供应的缓冲作用，电解槽可在电力盈余时与储能系统配合控制电力平衡，减少弃电。根据附图D1和D2，策略一与策略二在制氢功率分配策略上趋于一致，但在精确控制方面有所不同。策略二中电解水制氢装置1~4的周排产计划(见附图D4)显示，前两天(1~48时段)新能源出力充足，电解水制氢装置运行接近额定功率；在第3天至第7天(49~168时段)，新能源出力不足时，通过多电解槽协同操作，使其工作在最大效率功率点附近。比较策略一和策略二的结果，策略二通过效率曲线的应用，使制氢综合效率从17.55提高至18.72，节约了6.25%的电能。

3.2.4 不同中长期分解曲线对系统配置的影响

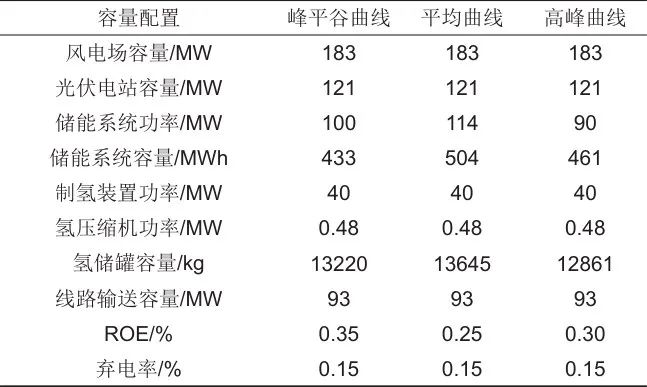
针对3种不同的负荷曲线分解方法，其具体配置方案见表5。峰谷平曲线法所获得的收益最高，其次是高峰时段曲线法，而全天平均曲线法的收益最低。这一结果进一步表明，适度合理的拉开峰谷价差可以显著提升新能源场站的盈利能力，激励其通过增加灵活调节手段积极参与市场。

表5   不同分解曲线对应的配置方案

4 结论

本文聚焦新能源发电独立参与电力市场的难题，重点探究风-光-储-氢混合电厂的最优容量配置。通过构建多种方案并运用规划算法分析，发现混合电厂配置方案(方案一)在保障经济效益的同时，满足了电力与氢能双重负荷需求，综合效益和投资潜力显著。采用本文研究的算法优化配置后的方案一，ROE达到了0.32，高于其他方案的运行模式；考虑电解水制氢装置效率特性的规划运行策略，能高效利用新能源电力制氢，将ROE提升至0.35；峰谷平曲线法模式下，混合电厂ROE最高，电力市场环境下适度拉开峰谷价差，可以提升混合电厂的盈利能力。同时，混合电厂中异质能量之间的互补与转化，增强了其应对电力市场价格波动和能源需求不确定性的灵活调节能力，优化资源配置和储能调度可将新能源弃电率控制在15%以内。本文提出的混合电厂方案及其配置方法，可以为新能源发电独立参与电力市场提供支撑。